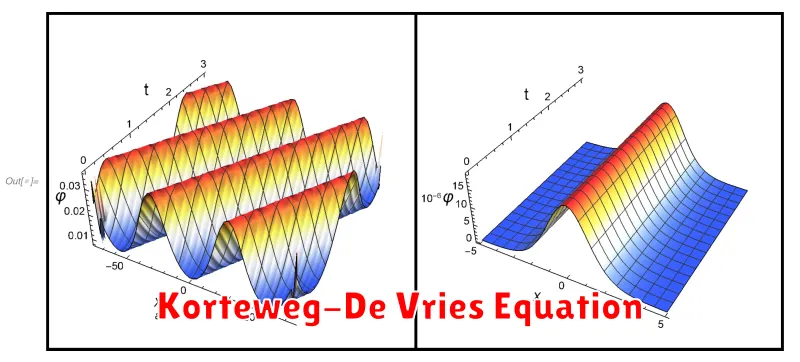
Persamaan Korteweg-de Vries, yang sering disingkat sebagai persamaan KdV, adalah salah satu persamaan diferensial parsial yang signifikan dalam bidang matematika terapan. Persamaan ini pertama kali diperkenalkan oleh Diederik Korteweg dan Gustav de Vries pada akhir abad ke-19. Persamaan KdV menjadi fundamental dalam memodelkan fenomena soliton dalam fluida, yang merupakan gelombang soliter dengan sifat luar biasa dalam propagasi tanpa kehilangan bentuknya. Pemahaman mendalam mengenai persamaan KdV memberikan wawasan penting dalam berbagai aplikasi sains dan teknik, seperti dalam hidrodinamika dan optik nonlinier.
Artikel ini akan membahas secara komprehensif mengenai pengertian Persamaan Korteweg-de Vries dalam matematika, dari latar belakang sejarah, konsep dasar, hingga penerapannya dalam berbagai disiplin ilmu. Kami akan mengulas bagaimana persamaan ini terbentuk dan mengapa ia memainkan peran penting dalam studi tentang gelombang dan dinamika fluida. Dengan penjelasan yang disajikan, diharapkan pembaca dapat memperoleh pemahaman yang lebih jelas tentang relevansi dan pentingnya persamaan KdV dalam konteks modern dan aplikatif.
Pendahuluan
Dalam matematika, terdapat berbagai persamaan diferensial yang berfungsi untuk menyelesaikan masalah dalam fisika dan teknik. Salah satu persamaan diferensial yang terkenal adalah Persamaan Korteweg-de Vries (KdV). Persamaan ini sangat penting dalam memodelkan fenomena fisika tertentu, terutama dalam bidang non-linear wave theory atau teori gelombang non-linear.
Persamaan Korteweg-de Vries pertama kali diperkenalkan oleh dua matematikawan Belanda, yaitu Diederik Korteweg dan Gustav de Vries, pada akhir abad ke-19. Mereka mengembangkan persamaan ini untuk menggambarkan gelombang soliton di saluran air yang dangkal. Sejak saat itu, KdV telah diterapkan dalam berbagai penelitian dan aplikasi ilmiah.
Artikel ini bertujuan untuk memberikan pemahaman mendalam mengenai pengertian dan aplikasi Persamaan Korteweg-de Vries dalam bidang matematika dan fisika. Dengan memahami dasar-dasar persamaan ini, diharapkan pembaca dapat menghargai pentingannya dalam analisis fenomena gelombang non-linear dan aplikasi ilmu yang lebih luas.
Sejarah Persamaan Korteweg-de Vries
Persamaan Korteweg-de Vries, yang sering disingkat sebagai persamaan KdV, pertama kali diperkenalkan oleh dua ilmuwan dari Belanda, Diederik Korteweg dan Gustav de Vries, pada tahun 1895. Mereka mempublikasikan temuan ini dalam jurnal yang berjudul “On the Change of Form of Long Waves Advancing in a Rectangular Canal, and on a New Type of Long Stationary Waves.”
Konsep di balik persamaan KdV berasal dari pengamatan terhadap gelombang air panjang yang bergerak melalui kanal sempit. Korteweg dan de Vries berusaha memahami bagaimana gelombang ini berubah bentuk ketika bergerak dan menemukan bahwa persamaan diferensial parsial nonlinear ketiga ini dapat digunakan untuk memodelkan fenomena tersebut.
Penemuan ini memiliki signifikansi yang besar dalam ilmu pengetahuan, terutama dalam bidang matematika terapan dan fisika fluida. Persamaan KdV menjadi landasan penting dalam studi tentang soliton, yakni gelombang yang mempertahankan bentuknya saat bergerak dengan kecepatan konstan. Penemuan soliton ini kemudian membawa dampak besar pada berbagai bidang seperti optik dan teori medan kuantum.
Baru pada tahun 1960-an dan 1970-an, persamaan KdV mendapatkan perhatian lebih luas dalam komunitas ilmiah ketika Kruskal dan Zabusky menemukan bahwa solusi persamaan KdV dapat ditentukan melalui metode analitis yang dikenal sebagai transformasi invers Boltzmann. Penemuan ini membuka jalan bagi penelitian lebih lanjut dalam mempelajari perilaku nonlinear dinamis.
Secara keseluruhan, persamaan Korteweg-de Vries tidak hanya mendefinisikan ulang pemahaman kita tentang gelombang dan soliton, tetapi juga memperkaya bidang matematika terapan dengan aplikasi yang luas dan mendalam. Hingga kini, persamaan KdV tetap menjadi topik yang aktif dipelajari dan dikembangkan dalam berbagai disiplin ilmu.
Bentuk Umum Persamaan Korteweg-de Vries
Persamaan Korteweg-de Vries, yang sering disingkat sebagai persamaan KdV, adalah salah satu persamaan diferensial yang paling penting dalam bidang matematika dan fisika. Persamaan ini digunakan untuk menggambarkan gelombang soliton, yang bisa dipertahankan bentuknya saat bergerak dengan kecepatan tetap.
Bentuk umum dari persamaan Korteweg-de Vries adalah:
(frac{partial u}{partial t} + 6ufrac{partial u}{partial x} + frac{partial^3 u}{partial x^3} = 0)
Dalam persamaan ini, u adalah fungsi dari dua variabel yakni x (posisi) dan t (waktu). Komponen (frac{partial u}{partial t}) menggambarkan perubahan fungsi terhadap waktu, sementara (frac{partial u}{partial x}) dan (frac{partial^3 u}{partial x^3}) menggambarkan perubahan terhadap posisi.
Persamaan ini pertama kali diperkenalkan oleh D.J. Korteweg dan G. de Vries pada tahun 1895, untuk menjelaskan fenomena gelombang soliton dalam kanal air. Sejak saat itu, persamaan KdV telah diterapkan dalam banyak bidang lain, termasuk optik, plasma, dan bahkan biologi.
Aplikasi Persamaan Korteweg-de Vries
Persamaan Korteweg-de Vries (K-dV) memiliki berbagai aplikasi yang signifikan dalam berbagai bidang ilmu. Salah satu aplikasi pentingnya adalah dalam memahami dan memodelkan soliton, gelombang nonlinier yang mempertahankan bentuknya saat bergerak. Ini sangat relevan dalam fisika fluida.
Selain itu, K-dV juga diaplikasikan dalam optik nonlinier untuk menjelaskan fenomena gelombang cahaya dalam serat optik. Persamaan ini membantu dalam pengembangan teknologi komunikasi serat optik yang mampu mengirimkan data dengan kecepatan dan kejernihan tinggi.
Dalam meteorologi, persamaan K-dV digunakan untuk memodelkan gelombang di atmosfer dan di lautan. Gelombang atmosfer dan laut dapat dianalisis menggunakan solusi soliton dari persamaan ini, yang membantu dalam memprediksi perilaku cuaca ekstrem dan sistem gelombang laut.
Secara matematis, K-dV juga digunakan dalam teori medan kuantum dan pengembangan model untuk menggambarkan dinamika sistem fisik yang kompleks. Ini memberikan wawasan mendalam tentang interaksi partikel dalam berbagai skala.
Dengan aplikasi yang luas dan beragam ini, K-dV menjadi alat penting dalam pemahaman berbagai fenomena alam dan teknologi canggih, memperlihatkan relevansi abadi dari persamaan ini dalam kemajuan ilmu pengetahuan dan teknologi.
Metode Penyelesaian Persamaan Korteweg-de Vries
Persamaan Korteweg-de Vries (KdV) adalah salah satu persamaan diferensial parsial penting dalam bidang matematika terapan dan fisika. Persamaan ini seringkali digunakan untuk mendeskripsikan gelombang soliton dalam media kontinu, termasuk air dangkal.
Untuk menyelesaikan persamaan KdV, terdapat beberapa metode yang dapat digunakan. Salah satu metode yang popular adalah metode transformasi inversi atau Inverse Scattering Transform (IST). Metode IST memungkinkan kita untuk mengubah persamaan diferensial nonlinear menjadi serangkaian persamaan linear yang lebih mudah diselesaikan.
Langkah pertama dalam metode IST adalah mentransformasikan persamaan KdV ke dalam bentuk yang dapat dikerjakan menggunakan operator linear. Ini biasanya melibatkan penerapan transformasi Fourier. Setelah persamaan itu diubah, solusinya dapat diperoleh dengan cara menyusun kembali komponen linear yang telah disederhanakan tersebut.
Selain metode IST, pendekatan numerik juga sering digunakan untuk menyelesaikan persamaan KdV. Pendekatan ini meliputi algoritma finite difference dan metode elemen hingga, yang memungkinkan kita untuk menghitung solusi dalam bentuk diskret. Metode numerik ini sangat berguna dalam situasi di mana pendekatan analitik sulit atau tidak memungkinkan.
Dalam konteks penelitian dan aplikasi praktis, beberapa solusi khusus dari persamaan KdV seperti soliton sering menjadi fokus utama. Soliton adalah solusi dalam bentuk gelombang yang dapat bergerak stabil tanpa perubahan bentuk, suatu fenomena yang sangat menarik dalam dinamika fluida dan optik.