Matriks dalam Matematika adalah salah satu konsep yang sangat penting dan sering digunakan dalam berbagai cabang ilmu, termasuk fisika, ekonomi, statistika, dan teknik. Pemahaman yang baik tentang matriks tidak hanya membantu dalam menyelesaikan berbagai persamaan linear, tetapi juga dalam analisis data, transformasi geometris, dan bahkan pengolahan citra digital. Oleh karena itu, sangat penting untuk memahami pengertian matriks secara mendalam.
Artikel ini akan membahas secara rinci tentang definisi dan pengertian matriks, contoh-contoh penggunaan matriks dalam berbagai bidang, serta bagaimana mengoperasikan matriks dalam matematika modern. Dengan memperhatikan pembahasan ini, diharapkan pembaca dapat memahami konsep dasar dari matriks dan bisa mengaplikasikannya dalam berbagai permasalahan yang membutuhkan analisis numerik dan aljabar. Jangan lewatkan informasi berharga tentang pengertian matriks dalam matematika yang akan membantu menambah wawasan Anda.
Apa itu Matriks?
Matriks adalah suatu susunan atau tabel bilangan yang dirangkai dalam baris dan kolom dan digunakan dalam berbagai cabang matematika. Matriks biasa dinyatakan dalam bentuk persegi panjang, yang memiliki elemen-elemen yang diatur dalam baris (rows) dan kolom (columns).
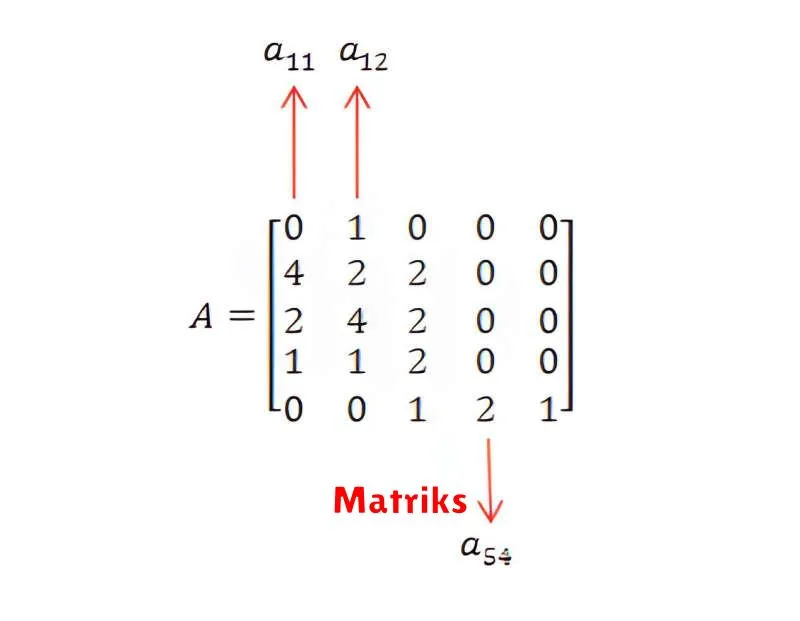
Setiap elemen dalam matriks diindeks oleh dua indeks, yaitu indeks baris dan indeks kolom. Notasi umum untuk suatu matriks adalah dengan huruf besar, seperti A, sementara elemen-elemen di dalamnya dinotasikan dengan huruf kecil dua subskrip, misalnya aij, yang berarti elemen pada baris ke-i dan kolom ke-j dalam matriks A.
Matriks dapat memiliki berbagai ukuran, yang disebut juga dengan dimensi. Dimensi matriks dinyatakan sebagai m x n, dimana m adalah jumlah baris dan n adalah jumlah kolom. Misalnya, matriks berukuran 2 x 3 berarti matriks tersebut memiliki 2 baris dan 3 kolom.
Penggunaan matriks sangat luas dalam banyak bidang, termasuk sains, teknik, serta ekonomi. Matriks digunakan untuk menyelesaikan sistem persamaan linear, melakukan transformasi geometris, dan dalam berbagai aplikasi komputasi lainnya.
Jenis-jenis Matriks
Dalam matematika, matriks memiliki berbagai jenis berdasarkan karakteristik dan elemen-elemennya. Memahami jenis-jenis matriks sangat penting untuk aplikasi dalam berbagai bidang seperti aljabar linear, fisika, dan ilmu komputer.
Salah satu jenis matriks yang paling umum adalah matriks persegi. Matriks ini memiliki jumlah baris yang sama dengan jumlah kolom. Misalnya, matriks berukuran 3×3 adalah contoh dari matriks persegi. Matriks ini sering digunakan dalam operasi determinan dan invers.
Jenis lain dari matriks adalah matriks identitas. Matriks ini merupakan matriks persegi di mana semua elemen diagonalnya adalah satu, sedangkan elemen lainnya adalah nol. Matriks identitas sering dilambangkan dengan huruf I dan memainkan peran penting dalam operasi matriks karena fungsinya seperti angka satu dalam perkalian.
Matriks diagonal adalah matriks yang memiliki elemen nol di luar diagonal utamanya dan elemen tak nol di diagonal utama. Matriks ini digunakan dalam berbagai operasi matematis yang memerlukan penyederhanaan perhitungan.
Selain itu, terdapat matriks segitiga yang dapat dibagi menjadi dua kategori: matriks segitiga atas dan matriks segitiga bawah. Matriks segitiga atas memiliki elemen nol di bawah diagonal utama, sedangkan matriks segitiga bawah memiliki elemen nol di atas diagonal utama. Matriks segitiga ini sering digunakan dalam metode factorizasi matriks.
Terakhir, ada matriks nol, yang semua elemen-elemennya adalah nol. Walaupun tampak sederhana, matris nol sering digunakan dalam banyak operasi dasar dan lanjutan dalam matriks.
Operasi pada Matriks
Matriks merupakan elemen penting dalam matematika yang digunakan untuk menyederhanakan dan menyelesaikan masalah kompleks. Operasi pada matriks melibatkan berbagai metode yang digunakan untuk melakukan perhitungan matematis antara satu matriks dengan matriks lainnya.
Salah satu operasi dasar pada matriks adalah penjumlahan dan pengurangan. Untuk melakukan penjumlahan atau pengurangan matriks, kedua matriks harus memiliki ukuran yang sama. Elemen-elemen yang bersesuaian dari kedua matriks tersebut kemudian dijumlahkan atau dikurangkan.
Operasi berikutnya adalah perkalian matriks. Perkalian ini tidak seperti penjumlahan atau pengurangan karena tidak hanya melibatkan operasi di antara elemen-elemen seposisi. Untuk melakukannya, kita harus mengalikan elemen dari baris matriks pertama dengan elemen dari kolom matriks kedua, kemudian menjumlahkan hasilnya untuk mendapatkan elemen baru dalam matriks hasil.
Selain itu, terdapat operasi yang dikenal sebagai transpos matriks. Operasi ini mengubah baris pada matriks menjadi kolom dan sebaliknya. Misalnya, jika sebuah matriks memiliki dimensi m x n, maka transposnya akan memiliki dimensi n x m.
Untuk menyelesaikan sistem persamaan linear, dapat digunakan invers matriks. Invers matriks adalah matriks lain yang ketika dikalikan dengan matriks asli, menghasilkan matriks identitas. Tidak semua matriks memiliki invers, hanya matriks persegi yang mempunyai invers.
Dengan memahami dan menguasai berbagai operasi pada matriks, para matematikawan dan ilmuwan dapat lebih mudah dalam memecahkan beraneka ragam persoalan yang melibatkan matriks dalam berbagai bidang, termasuk fisika dan teknik.
Penggunaan Matriks dalam Kehidupan Sehari-hari
Matriks adalah suatu susunan bilangan berbentuk persegi panjang atau persegi yang terorganisir dalam baris dan kolom. Matriks memiliki peran penting dalam berbagai aspek kehidupan sehari-hari, baik dalam bidang teknologi maupun dalam aplikasi praktis lainnya.
Salah satu penggunaan nyata dari matriks adalah dalam grafis komputer. Dalam pengolahan gambar dan pembuatan animasi, matriks digunakan untuk melakukan transformasi seperti rotasi, translasi, dan penskalaan objek. Matriks juga memungkinkan pengembangan teknologi augmented reality dan virtual reality, yang semakin populer dalam berbagai industri.
Di bidang teknik elektro, matriks digunakan dalam analisis rangkaian listrik. Dengan menggunakan matriks, insinyur dapat menyederhanakan perhitungan kompleks yang diperlukan untuk menentukan aliran arus dan tegangan dalam rangkaian. Ini sangat penting dalam desain dan optimalisasi peralatan elektronik.
Pada manajemen data, matriks digunakan dalam pengelolaan basis data. Matriks membantu mengatur dan mengakses data secara efisien, memungkinkan pemrosesan data yang cepat dan akurat. Algoritma pencarian dan pengurutan data juga sering kali bergantung pada operasi matriks.
Selain itu, dalam bidang ekonomi dan keuangan, matriks digunakan untuk menggerakkan analisis risiko, optimisasi portofolio, serta penghitungan input-output dalam model ekonomi. Matriks membantu dalam memetakan hubungan antar variabel ekonomi atau keuangan dan memfasilitasi perhitungan prediksi yang lebih akurat.
Penggunaan matriks dalam bidang kecerdasan buatan (AI) dan pembelajaran mesin (machine learning) juga sangat signifikan. Matriks digunakan untuk mengoperasikan data dalam algoritma pembelajaran, mengubah data input menjadi data output melalui berbagai lapisan jaringan saraf tiruan (artificial neural networks).