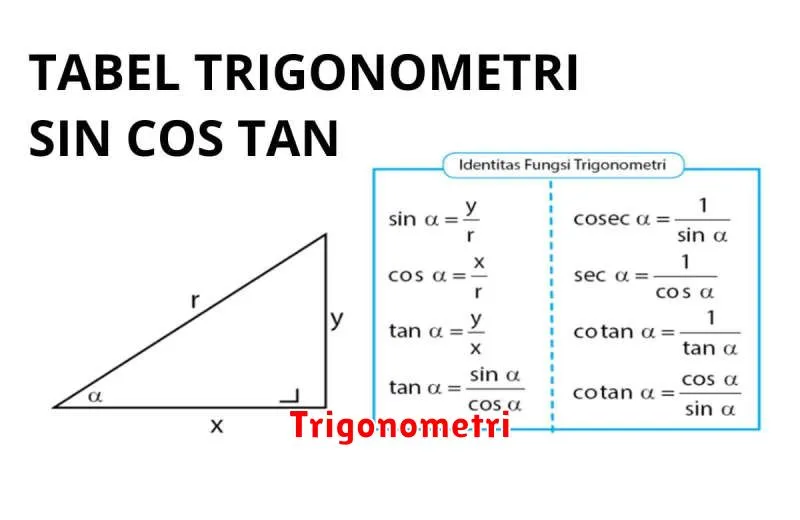
Dalam dunia matematika, identitas trigonometri memiliki peran yang sangat penting dan luas dalam berbagai aplikasi. Identitas trigonometri adalah rumus-rumus yang melibatkan fungsi-fungsi trigonometri seperti sinus, kosinus, dan tangen, yang digunakan untuk menyederhanakan dan menyelesaikan berbagai jenis masalah matematika. Rumus-rumus ini tidak hanya penting untuk keperluan akademis, tetapi juga sangat berguna dalam berbagai bidang seperti fisika, teknik, dan astronomi.
Artikel ini akan membahas secara mendalam mengenai identitas trigonometri, mulai dari pengertian dasar, rumus-rumus fundamental, hingga aplikasi praktis dalam kehidupan sehari-hari. Bagi pembaca yang ingin memperdalam pemahaman tentang trigonometri, membaca artikel ini dapat memberikan wawasan yang berharga serta memperkaya pengetahuan. Mari kita jelajahi lebih lanjut bagaimana identitas trigonometri berfungsi dan bagaimana kita dapat mengaplikasikannya dalam berbagai situasi.
Apa Itu Identitas Trigonometri?
Identitas trigonometri adalah persamaan yang melibatkan fungsi-fungsi trigonometri dan yang berlaku untuk setiap nilai sudut. Identitas ini sangat penting dalam matematika dan fisika karena memungkinkan kita untuk menyederhanakan perhitungan dan memahami hubungan antara berbagai fungsi trigonometri.
Secara umum, identitas trigonometri digunakan untuk mengubah satu bentuk trigonometri menjadi bentuk lain yang lebih sederhana atau lebih sesuai untuk penyelesaian tertentu. Beberapa identitas trigonometri dasar yang sering digunakan mencakup identitas Pythagoras, identitas sudut ganda, dan identitas sudut setengah.
Identitas ini juga memainkan peran utama dalam analisis matematika, khususnya dalam memecahkan persamaan trigonometri yang kompleks, integral trigonometri, dan persamaan diferensial. Dengan menggunakan identitas trigonometri, kita dapat menyelesaikan masalah yang awalnya tampak rumit menjadi lebih mudah dipecahkan.
Rumus-Rumus Dasar Identitas Trigonometri
Dalam dunia matematika, identitas trigonometri memainkan peranan yang sangat penting. Identitas trigonometri adalah rumus-rumus yang menyatakan hubungan antara fungsi-fungsi trigonometri. Pemahaman terhadap rumus dasar ini sangat diperlukan dalam banyak aplikasi matematis baik di bidang teknik, fisika, maupun komputasi.
Salah satu identitas trigonometri yang paling mendasar adalah identitas Pitagoras. Identitas ini menyatakan bahwa untuk setiap sudut ( theta ), berlaku rumus berikut:
sin²(θ) + cos²(θ) = 1
Selain identitas Pitagoras, ada juga identitas tolak tambah sudut yang sering digunakan. Rumus ini sangat berguna untuk menghitung nilai fungsi trigonometri dari jumlah atau selisih dua sudut. Contoh identitas tolak tambah sudut adalah:
sin(α ± β) = sin(α)cos(β) ± cos(α)sin(β)
cos(α ± β) = cos(α)cos(β) ∓ sin(α)sin(β)
Sementara itu, identitas trigonometri ganda membantu dalam menyederhanakan perhitungan trigonometri. Berikut adalah contoh identitas trigonometri ganda:
sin(2θ) = 2sin(θ)cos(θ)
cos(2θ) = cos²(θ) - sin²(θ)
Memahami rumus-rumus dasar ini adalah langkah awal yang penting dalam menguasai trigonometri secara menyeluruh. Penggunaan identitas-identitas ini bisa membantu dalam menyelesaikan berbagai masalah, baik dalam konteks akademis maupun aplikasi praktis.
Identitas Sudut Rangkap dan Setengah Sudut
Dalam dunia matematika, khususnya pada cabang trigonometri, identitas sudut rangkap dan setengah sudut memegang peranan penting dalam menyederhanakan perhitungan dan pemahaman konsep-konsep yang lebih kompleks. Rumus-rumus ini membantu dalam merumuskan dan menyelesaikan berbagai masalah matematika dengan lebih efisien.
Identitas sudut rangkap mengacu pada rumus trigonometri yang menggandakan suatu sudut. Misalnya, untuk sudut θ, rumus-rumus pentingnya adalah:
- Sin 2θ = 2sinθcosθ
- Cos 2θ = cos²θ – sin²θ atau 2cos²θ – 1 atau 1 – 2sin²θ
- Tan 2θ = 2tanθ / (1 – tan²θ)
Rumus-rumus ini memungkinkan kita untuk mengubah persamaan trigonometri dengan sudut rangkap ke dalam bentuk yang lebih sederhana atau lebih mudah dihitung.
Sementara itu, identitas setengah sudut digunakan untuk membagi sudut menjadi dua bagian. Contoh rumus untuk sudut setengah adalah:
- Sin (θ/2) = ±√((1 – cosθ)/2)
- Cos (θ/2) = ±√((1 + cosθ)/2)
- Tan (θ/2) = ±√((1 – cosθ)/(1 + cosθ)) atau Sinθ/(1 + cosθ)
Penggunaan tanda ± di sini menunjukkan bahwa nilai hasil rumus tergantung pada kuadran sudut tersebut berada. Identitas ini sangat berguna saat kita perlu menghitung nilai trigonometri dari sudut yang lebih kecil atau untuk penyederhanaan integral trigonometri.
Secara keseluruhan, identitas sudut rangkap dan setengah sudut adalah alat penting dalam trigonometri yang menawarkan solusi praktikal untuk masalah matematika kompleks. Pemahaman dan pemanfaatan rumus-rumus ini bisa meningkatkan efisiensi dan ketepatan dalam perhitungan.
Identitas Jumlah dan Selisih Dua Sudut
Dalam matematika, khususnya dalam bidang trigonometri, identitas jumlah dan selisih dua sudut memainkan peran yang sangat penting. Identitas ini memungkinkan kita untuk menghitung nilai fungsi trigonometri dari jumlah dua sudut atau selisih dua sudut dengan lebih mudah.
Rumus identitas jumlah dua sudut untuk fungsi sinus dan kosinus adalah sebagai berikut:
- Sin(α + β) = Sin(α)Cos(β) + Cos(α)Sin(β)
- Cos(α + β) = Cos(α)Cos(β) – Sin(α)Sin(β)
Rumus identitas selisih dua sudut untuk sinus dan kosinus adalah:
- Sin(α – β) = Sin(α)Cos(β) – Cos(α)Sin(β)
- Cos(α – β) = Cos(α)Cos(β) + Sin(α)Sin(β)
Dengan menggunakan rumus-rumus ini, kita dapat menyederhanakan perhitungan dan memecahkan berbagai macam masalah trigonometri secara lebih efisien. Pemahaman yang mendalam tentang identitas jumlah dan selisih dua sudut sangat penting bagi siswa dan profesional yang terlibat dalam bidang matematika dan sains.
Pembuktian Identitas Trigonometri
Identitas trigonometri adalah rumus yang menunjukkan hubungan tertentu antara fungsi trigonometri, seperti sinus, kosinus, dan tangen. Pembuktian identitas trigonometri melibatkan penggunaan definisi dasar dan sifat-sifat dari fungsi-fungsi ini untuk menunjukkan bahwa hubungan tersebut benar untuk semua nilai yang diizinkan dari variabel.
Salah satu contoh identitas trigonometri adalah Pythagorean Identity, yang menyatakan bahwa untuk setiap sudut θ, berlaku:
sin²(θ) + cos²(θ) = 1
Pembuktian dari identitas ini dapat dilakukan dengan menggunakan teorema Pythagoras pada segitiga siku-siku. Misalkan sebuah segitiga siku-siku dengan panjang sisi miring 1, maka panjang sisi-sisi lainnya dapat dinyatakan dalam bentuk fungsi trigonometri:
- Panjang sisi berhadapan dengan sudut θ adalah sin(θ).
- Panjang sisi yang bersebelahan dengan sudut θ adalah cos(θ).
Dengan menggunakan teorema Pythagoras (a² + b² = c²) pada segitiga tersebut, kita mendapatkan persamaan:
sin²(θ) + cos²(θ) = 1², yang berarti sin²(θ) + cos²(θ) = 1.
Contoh lain dari identitas trigonometri adalah tangen dalam bentuk sinus dan kosinus, yang dapat dinyatakan sebagai:
tan(θ) = sin(θ) / cos(θ)
Untuk membuktikan identitas ini, kita perlu melihat definisi dari tan(θ) sebagai perbandingan sisi pada segitiga siku-siku, yang berarti:
tan(θ) = Opposite / Adjacent.
Kemudian, karena sin(θ) = Opposite / Hypotenuse dan cos(θ) = Adjacent / Hypotenuse, maka:
tan(θ) = (Opposite / Hypotenuse) / (Adjacent / Hypotenuse) = sin(θ) / cos(θ).
Pembuktian identitas trigonometri seperti ini sangat penting dalam matematika karena memungkinkan kita untuk menyederhanakan dan memecahkan berbagai jenis persamaan trigonometri.
Penggunaan Identitas Trigonometri dalam Menyelesaikan Persamaan
Identitas trigonometri merupakan alat yang sangat berguna dalam menyelesaikan persamaan trigonometri. Dengan menggunakan identitas ini, kita dapat menyederhanakan dan memecahkan masalah yang sebelumnya tampak rumit. Salah satu identitas trigonometri yang sering digunakan adalah identitas Pythagoras yang berbunyi sin²θ + cos²θ = 1.
Selain identitas Pythagoras, identitas sudut rangkap seperti 2sinθcosθ = sin2θ dan cos²θ – sin²θ = cos2θ juga sering diterapkan. Identitas ini memungkinkan kita untuk mengubah bentuk persamaan menjadi lebih sederhana, sehingga lebih mudah untuk mencari nilai variabel yang diinginkan.
Contohnya, dalam menyelesaikan persamaan sin2θ = √3 / 2, kita dapat memanfaatkan identitas sudut rangkap yang mengubah persamaan tersebut menjadi 2sinθcosθ = √3 / 2. Selanjutnya, kita dapat menyelesaikan persamaan ini dengan mencari nilai sinθ dan cosθ yang memenuhi kondisi tersebut.
Penerapan identitas trigonometri tidak hanya terbatas pada penyelesaian persamaan sederhana. Dalam kasus yang lebih kompleks, kombinasi berbagai identitas mungkin diperlukan untuk mencapai solusi akhir. Identitas trigonometri juga sering digunakan dalam analisis fungsi periodik, pemodelan gelombang, dan berbagai aplikasi fisika serta teknik.
Kesimpulannya, memahami dan menguasai identitas trigonometri adalah keterampilan penting yang dapat memperluas kemampuan seseorang dalam menyelesaikan masalah matematika yang kompleks. Dengan kemampuan ini, berbagai jenis persamaan trigonometri dapat diselesaikan dengan lebih efisien dan akurat.
Aplikasi Identitas Trigonometri dalam Berbagai Bidang
Dalam dunia matematika dan sains, identitas trigonometri memiliki peran yang sangat penting. Identitas ini tidak hanya berguna dalam penyelesaian masalah teoritis, tetapi juga memiliki berbagai aplikasi praktis dalam berbagai bidang.
Salah satu aplikasi utama identitas trigonometri adalah dalam bidang fisika. Dalam analisis gerak harmonis sederhana, seperti gerak bandul atau gelombang, identitas trigonometri digunakan untuk memodelkan dan menganalisis perilaku sistem tersebut. Contoh lainnya adalah dalam mekanika kuantum di mana fungsi gelombang sering kali diekspresikan menggunakan fungsi trigonometri.
Dalam bidang teknik sipil dan arsitektur, identitas trigonometri membantu dalam perhitungan desain struktur bangunan. Misalnya, dalam menentukan panjang dan sudut material pendukung seperti balok dan kolom, serta dalam perhitungan kekuatan struktur terhadap beban.
Di bidang astronomi, identitas trigonometri digunakan untuk menghitung posisi bintang-bintang dan planet-planet relatif terhadap Bumi. Proses seperti triangulasi bintang untuk menentukan jarak antar objek astronomi sangat bergantung pada penggunaan trigonometri.
Pada bidang informatika dan grafika komputer, identitas trigonometri digunakan dalam algoritma untuk rendering gambar tiga dimensi, animasi, dan simulasi fisika. Penerapan ini memungkinkan pembuatan efek visual yang realistis dalam video game dan film animasi.
Dengan demikian, jelas terlihat bahwa pemahaman dan penerapan identitas trigonometri memiliki dampak luas yang signifikan dalam berbagai disiplin ilmu. Penguasaan konsep dasar ini tidak hanya bermanfaat dalam menyelesaikan masalah-masalah matematika tetapi juga memberikan solusi nyata dalam berbagai konteks praktis.