Dalam geometri dan matematika, konsep vektor merupakan salah satu elemen fundamental yang sering digunakan untuk merepresentasikan berbagai jenis data. Vektor memiliki karakteristik yang unik, yaitu memiliki magnitude (besaran) dan direction (arah) yang memungkinkannya untuk dipakai dalam berbagai aplikasi, mulai dari fisika hingga ilmu komputer. Pemahaman tentang pengertian vektor dalam geometri sangat penting karena vektor seringkali menjadi dasar dalam mempelajari dan menyelesaikan berbagai masalah matematika yang kompleks.
Artikel ini akan membahas secara rinci tentang pengertian vektor dalam geometri dan bagaimana konsep ini diterapkan dalam bidang matematika. Sebagai landasan penting dalam berbagai cabang ilmu, penguasaan materi tentang vektor akan memberikan pemahaman yang lebih baik dalam memahami struktur ruang dan berbagai fenomena yang dapat dimodelkan secara matematis. Tujuannya adalah untuk memberikan wawasan yang komprehensif serta memperkaya pengetahuan pembaca, terkhusus bagi mereka yang baru mengenal dunia geometri dan matematika.
Apa itu Vektor?
Vektor dalam geometri adalah sebuah besaran yang memiliki arah dan panjang. Vektor sering digunakan untuk merepresentasikan gerakan atau perubahan posisi dari satu titik ke titik lain dalam ruang.
Sebagai contoh, jika kita ingin mendeskripsikan perpindahan suatu objek, kita tidak hanya menyebutkan jaraknya tetapi juga arah perpindahannya. Itulah sebabnya vektor menjadi penting dalam berbagai aplikasi, termasuk fisika dan teknik.
Secara matematis, vektor dinyatakan dengan simbol panah, yang menunjukkan arah dan panjang atau magnitudo vektor tersebut. Panjang vektor dihitung menggunakan rumus yang melibatkan koordinat awal dan akhir vektor.
Pada dasarnya, materi ini bertujuan untuk membantu kita memahami bagaimana objek bergerak dan berinteraksi dalam ruang, serta menyediakan dasar untuk analisis dan pemecahan masalah yang lebih kompleks dalam matematika dan sains.
Notasi Vektor
Dalam geometri dan matematika, vektor adalah entitas yang memiliki besar dan arah. Notasi vektor biasanya digunakan untuk mewakili konsep ini secara simbolis, mempermudah pemahaman dan pengoperasian dalam berbagai konteks matematis.
Salah satu metode notasi vektor adalah dengan menggunakan huruf tebal, seperti v atau w. Alternatif lainnya adalah dengan huruf yang diberi tanda panah di atasnya, seperti →v atau →w, yang menjelaskan sifat arah dari vektor tersebut.
Dalam vektor dua dimensi, notasi umumnya diwakili dalam bentuk koordinat, misalnya v = (x, y), dimana x dan y adalah komponen vektor dalam sumbu X dan Y. Untuk vektor tiga dimensi, notasinya dituliskan sebagai v = (x, y, z) yang mencakup komponen dalam sumbu X, Y, dan Z.
Vektor juga dapat dinotasikan dalam bentuk komponen basis, yang sering ditulis sebagai v = xi + yj + zk. Di sini, i, j, dan k adalah vektor basis unit untuk sumbu X, Y, dan Z yang masing-masing memudahkan analisis dalam ruang tiga dimensi.
Notasi ini sangat penting karena memungkinkan representasi dan manipulasi yang jelas dan konsisten dari vektor dalam berbagai operasi matematis, seperti penjumlahan, pengurangan, dan perkalian skalar.
Elemen-Elemen Vektor: Arah dan Besar
Dalam geometri, elemen-elemen vektor menjadi komponen penting yang mendukung berbagai konsep matematika. Dua elemen utama yang mendefinisikan vektor adalah arah dan besar (magnitude). Pemahaman mendalam mengenai kedua elemen ini sangat penting bagi siswa dan praktisi bidang matematika serta ilmu pengetahuan terapan lainnya.
Arah adalah komponen yang menentukan ke mana vektor menunjuk dalam ruang. Dalam konteks dua dimensi, arah vektor dapat dipresentasikan dengan sudut yang dibentuk terhadap sumbu x. Pada ruang tiga dimensi, arah vektor membutuhkan lebih kompleksitas dengan penambahan sumbu z. Penting untuk memahami bahwa arah bukan hanya menunjukkan arah fisik tetapi juga berperan dalam komputasi matematika dan fisika.
Besar, atau juga dikenal sebagai magnitude, merupakan panjang vektor tersebut. Besar vektor dihitung menggunakan rumus geometris yang mendasarkan pada koordinat titik-titik pembentuknya. Dengan kata lain, besar vektor adalah ukuran jarak dari titik awal vektor ke titik akhirnya. Besar ini selalu merupakan bilangan tak negatif dan sering ditulis dengan simbol khusus, seperti |v|.
Kombinasi dari arah dan besar memberi kita pemahaman lengkap tentang vektor tersebut. Misalnya, dalam analisis gerak, arah dan besar vektor kecepatan memberi informasi lengkap tentang kecepatan objek dalam ruang. Dalam matematika, ini memungkinkan kita melakukan operasi seperti penjumlahan vektor, perkalian skalar, dan lain-lain, yang sangat berguna dalam memecahkan berbagai masalah geometri dan aljabar.
Jenis-Jenis Vektor
Dalam geometri dan matematika, vektor dapat dikategorikan menjadi beberapa jenis berdasarkan sifat dan aplikasi penggunaannya. Masing-masing jenis vektor memiliki karakteristik dan fungsi yang berbeda.
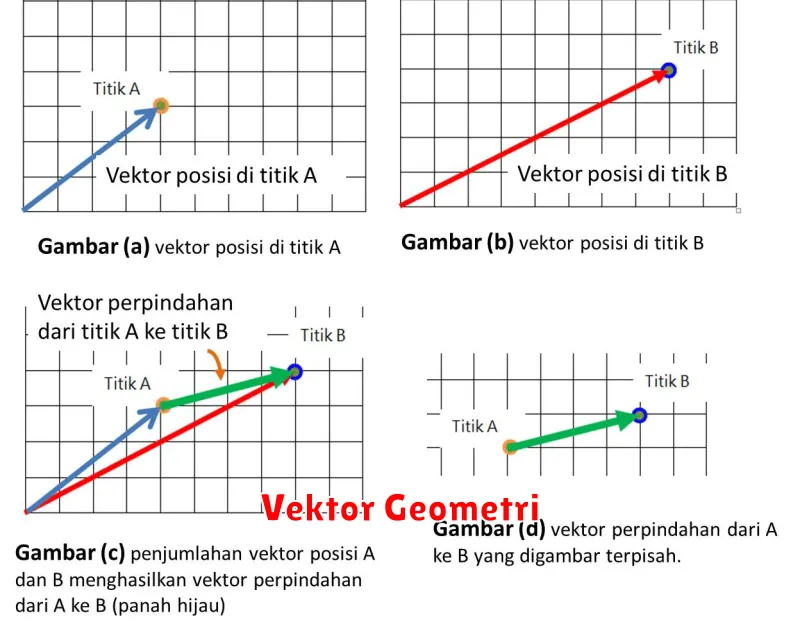
Vektor Posisi adalah jenis vektor yang menggambarkan posisi suatu titik relatif terhadap titik acuan, biasanya titik asal (0,0) dalam koordinat kartesian. Vektor ini digunakan untuk menunjukkan lokasi suatu titik di ruang dua atau tiga dimensi.
Vektor Bebas adalah vektor yang tidak terikat pada titik batas tertentu. Artinya, vektor ini fokus pada nilai dan arah, tanpa memperhatikan posisi awal atau akhirnya. Dengan demikian, vektor bebas dapat digeser parallel tanpa mengubah sifatnya.
Vektor Satuan adalah vektor dengan panjang atau magnitudo sebesar satu unit. Vektor ini sering digunakan untuk menunjukkan arah tertentu dalam ruang sambil tetap mempertahankan standar satuan panjang.
Vektor Basis adalah vektor yang berbentuk ortogonal dan ortonormal. Vektor ini sangat penting dalam ruang vektor, terutama dalam proses transformasi linear dan penentuan koordinat suatu titik dalam dimensi tertentu.
Vektor Kolinear adalah vektor-vektor yang sejajar atau berada pada garis yang sama. Jika dua atau lebih vektor memiliki arah yang sama atau berlawanan, maka mereka dikategorikan sebagai vektor kolinear.
Dengan memahami berbagai jenis vektor, kita dapat lebih mudah menganalisis dan memanipulasi parameter geometri dalam berbagai aplikasi matematika.
Operasi Vektor
Dalam geometri dan matematika, vektor merupakan objek yang memiliki besaran dan arah. Untuk memahami lebih dalam mengenai vektor, penting bagi kita untuk memahami berbagai operasi vektor yang sering digunakan dalam perhitungan matematika.
Salah satu operasi dasar pada vektor adalah penjumlahan vektor. Penjumlahan vektor dilakukan dengan menambahkan komponen-komponen yang bersesuaian dari kedua vektor. Misalkan terdapat dua vektor A dan B, maka hasil penjumlahannya adalah vektor C yang memiliki komponen-komponen (A₁ + B₁, A₂ + B₂).
Operasi lainnya adalah pengurangan vektor, yang mirip dengan penjumlahan, tetapi dilakukan dengan mengurangkan komponen yang bersesuaian. Jika terdapat vektor A dan B, maka hasil pengurangannya adalah vektor D dengan komponen (A₁ - B₁, A₂ - B₂).
Salah satu operasi penting dalam vektor adalah perkalian skalar. Perkalian skalar sebuah vektor dengan sebuah bilangan nyata menghasilkan sebuah vektor baru yang memiliki magnitudo yang berubah tetapi tetap sejajar dengan vektor awal. Misalnya, mengalikan vektor A dengan skalar k akan menghasilkan vektor dengan komponen (kA₁, kA₂).
Selain itu, terdapat produk titik dan produk silang. Produk titik dari dua vektor menghasilkan sebuah nilai skalar yang diperoleh dari penjumlahan hasil kali komponen yang bersesuaian. Sedangkan produk silang menghasilkan vektor yang tegak lurus terhadap dua vektor awal dan digunakan dalam konteks tiga dimensi.
Operasi-operasi ini sangat penting dalam berbagai bidang seperti fisika, teknik, dan ilmu komputer. Dengan memahami operasi dasar pada vektor, kita dapat menyelesaikan berbagai masalah yang melibatkan vektor dengan lebih mudah.
Penjumlahan dan Pengurangan Vektor
Dalam geometri dan matematika, vektor merupakan sebuah besaran yang mempunyai arah dan poin awal serta akhir yang berbeda. Oleh karena itu, penjumlahan dan pengurangan vektor menjadi konsep dasar yang sangat penting dalam memahami interaksi antar-vektor.
Untuk melakukan penjumlahan vektor, pertama-tama kita meletakkan ujung vektor pertama ke pangkal vektor kedua. Hasil dari penjumlahan dua vektor ini adalah sebuah vektor baru yang disebut sebagai “vektor hasil” atau “resultan”. Cara grafik ini sering kali disebut dengan metode poligon. Secara komponen, penjumlahan vektor dilakukan dengan menambahkan komponen-komponen yang bersesuaian dari kedua vektor. Misalnya, jika kita memiliki dua vektor, Vektor A = (?₁, ?₂) dan Vektor B = (?₁, ?₂), maka hasil penjumlahannya adalah Vektor C = (?₁ + ?₁, ?₂ + ?₂).
Pengurangan vektor, di sisi lain, dilakukan dengan cara yang serupa, hanya saja kita mengurangkan komponen-komponen yang bersesuaian. Sebagai contoh, jika ada dua vektor Vektor A dan Vektor B, pengurangannya dilakukan dengan komponen, sehingga Vektor D = (?₁ – ?₁, ?₂ – ?₂). Pengurangan vektor juga bisa dipahami sebagai penjumlahan dengan vektor yang mempunyai arah berlawanan.
Selain metode komponen, metode grafis juga sering digunakan dalam pengajaran konsep penjumlahan dan pengurangan vektor. Vektor-vektor digambarkan dalam sebuah segitiga atau jajaran genjang untuk memudahkan visualisasi proses penjumlahan atau pengurangan tersebut.
Perkalian Vektor dengan Skalar
Dalam geometri dan matematika, perkalian vektor dengan skalar adalah operasi yang penting dan banyak digunakan. Proses ini melibatkan pengalian suatu vektor dengan sebuah skalar, yang merupakan bilangan riil.
Perkalian ini menghasilkan vektor baru yang memiliki arah yang sama dengan vektor semula tetapi dengan panjang yang berubah sesuai dengan nilai skalar.
Misalnya, jika kita memiliki vektor v = (x, y) dan skalar k, maka hasil perkalian skalar tersebut adalah kv = (kx, ky). Dengan kata lain, setiap komponen dari vektor tersebut dikalikan dengan skalar.
Operasi ini berguna dalam berbagai aplikasi seperti rescaling vektor, mengubah panjang dan arah vektor dalam grafik komputer, dan dalam berbagai bidang ilmu fisika dan teknik.
Sebagai contoh, jika vektor a memiliki komponen (2, 3) dan skalar k bernilai 4, maka hasil perkaliannya adalah 4a = (8, 12). Ini menunjukkan bahwa panjang vektor diperbesar empat kali, namun arah vektor tetap sama.
Aplikasi Vektor dalam Kehidupan Sehari-hari
Vektor memiliki peran yang sangat penting dalam berbagai aspek kehidupan sehari-hari. Salah satu aplikasi yang paling nyata dari vektor adalah dalam bidang navigasi. Pemandu pesawat dan kapal menggunakan vektor untuk menentukan arah dan kecepatan perjalanan mereka. Dengan menggunakan vektor, mereka dapat memastikan bahwa mereka tetap berada pada jalur yang benar dan mencapai tujuan dengan efisien.
Selain itu, vektor digunakan dalam desain grafis dan animasi komputer. Software desain grafis seringkali menggunakan grafik vektor, yang memungkinkan desainer untuk membuat gambar yang dapat diubah ukurannya tanpa kehilangan kualitas. Ini sangat berguna dalam menghasilkan berbagai macam media, mulai dari logo perusahaan hingga animasi kompleks.
Dalam fisika dan rekayasa teknik, vektor digunakan untuk menggambarkan berbagai macam besaran seperti gaya, kecepatan, dan percepatan. Misalnya, dalam konstruksi bangunan, insinyur menggunakan konsep vektor untuk merancang struktur yang mampu menahan beban dan tekanan yang diterapkan.
Bahkan di bidang sistem informasi geografis (SIG), vektor adalah elemen kunci yang digunakan untuk merepresentasikan data geografis. Dengan bantuan peta vektor, kita dapat menyusun dan menganalisis data geografis dengan lebih mudah dan akurat, yang sangat penting dalam pembangunan tata kota dan perencanaan wilayah.
Dari contoh-contoh di atas, jelas bahwa vektor bukan hanya konsep matematika abstrak tetapi juga memiliki aplikasi yang luas dan langsung dalam kehidupan sehari-hari. Pemahaman yang baik mengenai vektor dapat membantu kita menjelaskan dan memecahkan berbagai permasalahan praktis yang kita hadapi sehari-hari.