Dalam matematika, khususnya pada bidang trigonometri, istilah sinus sering kali muncul dan memegang peranan yang sangat penting. Sinus adalah salah satu fungsi trigonometri yang paling dasar dan esensial. Fungsi ini digunakan untuk mengukur perbandingan antara panjang sisi miring dan panjang sisi berlawanan dalam sebuah segitiga siku-siku. Pemahaman yang mendalam tentang sinus akan membantu dalam menyelesaikan berbagai masalah yang terkait dengan sudut dan dimensi dalam trigonometri.
Artikel ini akan membahas lebih dalam mengenai pengertian sinus dalam trigonometri, serta bagaimana fungsi ini diaplikasikan dalam berbagai konteks matematis dan praktis. Dengan mengetahui pengertian dasar dari sinus, Anda akan lebih mudah memahami konsep-konsep lanjutan dalam trigonometri yang menggunakan fungsi ini. Ini adalah informasi yang sangat relevan bagi mereka yang tertarik dengan matematika atau bidang sains dan teknik secara lebih luas.
Apa itu Trigonometri?
Trigonometri adalah salah satu cabang dari matematika yang mempelajari hubungan antara panjang dan sudut dalam suatu segitiga. Istilah ini berasal dari bahasa Yunani, yaitu “trigonon” yang berarti segitiga, dan “metron” yang berarti mengukur.
Trigonometri memiliki peran penting dalam berbagai bidang, termasuk fisika, teknik, dan astronomi. Cabang ini membahas mengenai fungsi trigonometri seperti sinus, kosinus, dan tangen yang digunakan untuk menentukan nilai sudut dan panjang sisi pada segitiga.
Salah satu aplikasi utama trigonometri adalah dalam pemetaan dan navigasi. Dengan memahami konsep trigonometri, seseorang dapat dengan mudah menghitung jarak dan arah, serta memprediksi pergerakan benda dalam ruang.
Pemahaman dasar tentang trigonometri sangat penting dalam pendidikan matematika, terutama bagi siswa yang akan melanjutkan ke jenjang pendidikan lebih tinggi di bidang sains dan teknologi. Trigonometri membantu dalam mengembangkan keterampilan analitis dan pemecahan masalah yang kritis.
Pengertian Sinus
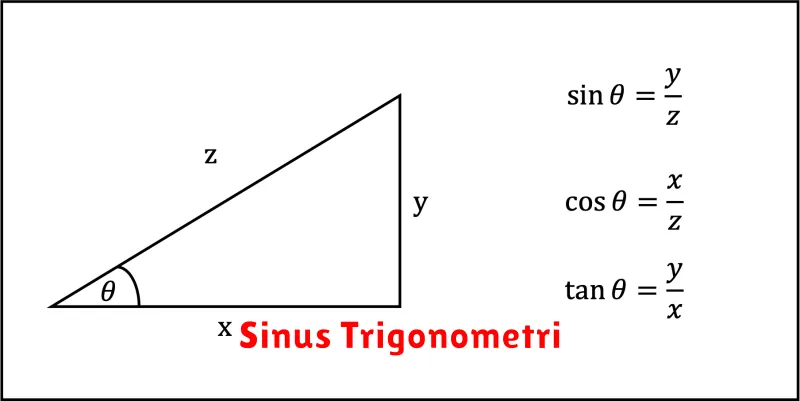
Dalam trigonometri, sinus adalah salah satu fungsi dasar yang digunakan untuk mengukur perbandingan sisi dalam sebuah segitiga siku-siku.
Fungsi sinus melibatkan perbandingan antara panjang sisi yang berlawanan dengan sudut tertentu (sisi bersebrang) dan panjang sisi miring (hipotenusa).
Secara matematis, sinus dari sudut θ dirumuskan sebagai sin(θ) = sisi bersebrang / hipotenusa.
Maka dari itu, fungsi sinus sangat berguna dalam berbagai aplikasi matematika dan fisika, seperti pengukuran sudut, solusi dari masalah geometris, dan analisis gelombang.
Sudut Istimewa dalam Sinus
Dalam trigonometri, terdapat beberapa Sudut Istimewa yang memiliki nilai sinus yang sudah diketahui secara pasti dan sering digunakan dalam berbagai aplikasi matematika. Sudut-sudut ini biasanya mencakup 0°, 30°, 45°, 60°, dan 90°.
Pada sudut 0°, nilai sinus adalah 0. Hal ini karena pada sudut ini, panjang sisi yang berseberangan dengan sudut tetap pada titik awal, sehingga tidak ada komponen vertikal dalam segitiga yang dihasilkan.
Sementara itu, pada sudut 30°, nilai sinus adalah 1/2. Karakteristik ini dapat dengan mudah dihafal dan sangat berguna dalam berbagai perhitungan trigonometri, terutama dalam menentukan posisi segitiga dan analisis vektor.
Untuk sudut 45°, nilai sinus adalah √2/2. Nilai ini sering muncul dalam konteks simetri dan digunakan dalam bidang teknik serta ilmu pengetahuan lainnya yang memerlukan ketepatan tinggi.
Selanjutnya, pada sudut 60°, nilai sinus adalah √3/2. Sudut 60° sering diidentifikasi dalam segitiga sama sisi, di mana semua sisi dan sudut adalah konstan.
Terakhir, pada sudut 90°, nilai sinus adalah 1. Ini adalah nilai maksimumnya karena pada sudut ini, sisi yang berseberangan dengan sudut menjadi sama dengan panjang hipotenusa segitiga itu sendiri, menciptakan segitiga dengan tinggi maksimal.
Dengan memahami dan menghafal nilai-nilai sinus pada Sudut Istimewa, seorang pelajar atau profesional dapat dengan mudah mempercepat perhitungan dan meningkatkan akurasi dalam berbagai aplikasi yang melibatkan trigonometri.
Grafik Fungsi Sinus
Fungsi sinus adalah salah satu fungsi trigonometri utama yang sering digunakan dalam matematika dan ilmu pengetahuan. Grafik fungsi sinus menunjukkan hubungan antara sudut dan nilai sinusnya, yang biasanya dinyatakan dalam radian atau derajat.
Grafik fungsi sinus berbentuk gelombang yang dikenal dengan istilah gelombang sinusoidal. Grafik ini memiliki bentuk yang berulang-ulang dengan periode sebesar 2π radian atau 360 derajat. Satu periode lengkap dari gelombang sinus meliputi kenaikan dari 0 ke maksimum, kembali ke 0, turun ke minimum, dan kembali lagi ke 0.
Sumbu horizontal pada grafik fungsi sinus biasanya mewakili sudut (baik dalam radian ataupun derajat), sedangkan sumbu vertikal mewakili nilai dari fungsi sinus. Amplitudo gelombang sinus adalah nilai maksimum atau minimum dari fungsi sinus, yang dalam bentuk standar adalah 1 atau -1.
Beberapa sifat penting dari grafik fungsi sinus adalah:
- Periode: Periode dari grafik sinus adalah jarak yang dibutuhkan untuk menyelesaikan satu siklus penuh, yaitu 2π radian.
- Amplitudo: Amplitudo mewakili besar maksimum dan minimum dari nilai fungsi sinus, yang dalam bentuk dasar adalah 1.
- Pergeseran Fase: Pergeseran fase mengacu pada pergeseran horizontal dari grafik. Fungsi sinus dapat bergeser ke kanan atau ke kiri tergantung pada nilai pergeseran fase yang ditambahkan atau dikurangkan.
- Pergeseran Vertikal: Pergeseran vertikal berarti grafik fungsi sinus bergeser ke atas atau ke bawah.
Grafik fungsi sinus sangat berguna dalam berbagai aplikasi, termasuk dalam fisika, teknik, dan analisis signal. Memahami karakteristik grafik ini memungkinkan kita untuk menginterpretasikan dan memanfaatkan data yang berkaitan dengan gelombang dan osilasi secara lebih efektif.
Hubungan Sinus dengan Fungsi Trigonometri Lainnya
Dalam bidang trigonometri, fungsi sinus tidak berdiri sendiri. Sinus memiliki hubungan yang erat dengan fungsi trigonometri lainnya seperti kosinus dan tangen. Hubungan ini dapat dilihat dari berbagai identitas trigonometri yang sering digunakan untuk menyelesaikan masalah-masalah matematika.
Salah satu identitas yang paling mendasar adalah identitas Pythagoras, yang menyatakan bahwa untuk setiap sudut θ dalam segitiga siku-siku, berlaku sin²(θ) + cos²(θ) = 1. Identitas ini menunjukkan bahwa nilai sinus dan kosinus untuk suatu sudut tertentu saling tergantung satu sama lain.
Selanjutnya, hubungan antara sinus dan tangen juga cukup signifikan. Dalam konteks segitiga siku-siku, tangen sebuah sudut diberikan oleh rasio sinus terhadap kosinus. Secara matematis, ini dapat dituliskan sebagai tan(θ) = sin(θ) / cos(θ). Hal ini memperkuat fakta bahwa memahami fungsi sinus tak lengkap tanpa memahami kosinus dan tangen.
Hubungan lainnya muncul dalam bentuk rumus tambahan sudut. Misalnya, sin(α + β) = sin(α)cos(β) + cos(α)sin(β). Rumus ini menunjukkan bagaimana sinus dari jumlah dua sudut dapat diuraikan menjadi kombinasinya dengan sinus dan kosinus dari sudut-sudut tersebut.
Selain itu, fungsi sinus juga memiliki hubungan dengan fungsi trigonometri lainnya seperti sekans dan kosekans. Sekans didefinisikan sebagai kebalikan kosinus, sementara kosekans didefinisikan sebagai kebalikan sinus, yaitu csc(θ) = 1/sin(θ).
Dengan memahami hubungan-hubungan ini, klarifikasi bagaimana fungsi trigonometri bekerja secara keseluruhan menjadi lebih jelas dan analisa matematis dapat dilakukan dengan lebih komprehensif dan efektif.
Aplikasi Sinus dalam Kehidupan Sehari-hari
Rumus sinus dalam trigonometri memiliki banyak aplikasi yang penting dalam kehidupan sehari-hari. Salah satu aplikasi utama adalah dalam bidang rekayasa dan teknik sipil. Di sini, perhitungan sudut dan panjang menggunakan rumus sinus sangat krusial dalam mendesain struktur bangunan, jembatan, dan berbagai infrastruktur lainnya. Akurasi pengukuran ini memastikan struktur tersebut stabil dan aman.
Selain itu, dalam navigasi laut dan udara, konsep sinus digunakan untuk menghitung lintasan dan menentukan posisi dalam sebuah peta. Penggunaan rumus sinus memungkinkan pilot dan kapten kapal untuk merencanakan rute yang efisien dan aman, serta untuk membuat penyesuaian ketika berhadapan dengan kondisi cuaca yang tidak terduga.
Aplikasi lain yang relevan adalah dalam teknologi satelit dan komunikasi. Satelit menggunakan prinsip trigonometri untuk menentukan posisinya di orbit dan untuk mengarahkan antena ke titik tertentu di bumi. Hal ini memungkinkan kualitas transmisi data dan sinyal yang lebih baik, yang sangat penting dalam komunikasi global.
Di bidang kedokteran, konsep sinus juga diterapkan, terutama dalam teknologi pencitraan medis seperti sinar-X dan MRI. Dengan menggunakan prinsip-prinsip trigonometri, dokter dapat memperoleh gambaran yang lebih jelas dan akurat dari organ dalam tubuh pasien, yang membantu dalam diagnosis dan perawatan yang tepat.