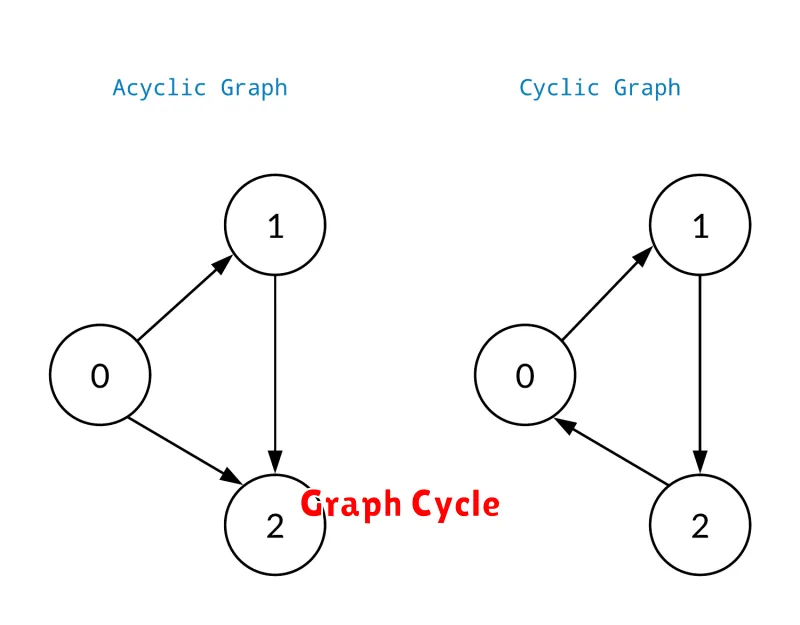
Dalam bidang matematika, teori graf merupakan salah satu topik yang sangat menarik dan penting untuk dipelajari. Salah satu konsep fundamental dalam teori graf adalah siklus. Memahami pengertian siklus dalam teori graf matematis adalah langkah kritis untuk memahami struktur dan sifat dari graf itu sendiri. Artikel ini akan mengupas tuntas apa yang dimaksud dengan siklus dalam konteks teori graf, serta pentingnya pemahaman ini dalam berbagai aplikasi praktis.
Siklus dalam sebuah graf dapat dijelaskan sebagai suatu jalur yang memulai dan mengakhiri perjalanannya pada simpul yang sama, tanpa melewati jalan yang sama lebih dari sekali. Konsep ini tidak hanya memperkaya pemahaman kita tentang graf secara teoretis, tetapi juga memiliki aplikatif dalam bidang seperti ilmu komputer, jaringan, dan rekayasa perangkat lunak. Melalui penjelasan yang komprehensif, kami berharap pembaca dapat memahami peran penting dari siklus dalam teori graf dan bagaimana konsep ini diterapkan dalam berbagai disiplin ilmu.
Definisi Graf
Dalam teori graf matematika, sebuah graf merupakan struktur yang digunakan untuk memodelkan pasangan hubungan antarelemen.
Graf terdiri dari simpul atau titik (vertex) dan rusuk atau sisi (edge) yang menghubungkan pasangan simpul tersebut.
Sebuah graf dapat direpresentasikan secara visual dengan menggunakan titik-titik yang dihubungkan oleh garis-garis, di mana setiap titik mewakili simpul dan setiap garis mewakili rusuk.
Graf digunakan dalam berbagai bidang, termasuk teknologi informasi, biologi, kimia, dan sosiologi, untuk memodelkan jaringan dan hubungan.
Dalam konteks matematika, studi tentang graf membantu dalam analisis struktur jaringan, optimasi jalur, dan penyusunan serta pemecahan masalah yang berkaitan dengan konektivitas dan aliran data.
Pemahaman mendalam mengenai definisi graf ini penting sebelum mempelajari konsep yang lebih kompleks seperti siklus dalam teori graf.
Pengertian Siklus dalam Graf
Dalam teori graf, siklus merupakan suatu path (jalur) yang menghubungkan simpul-simpul (node) dalam graf, di mana jalur tersebut berawal dari satu simpul dan kembali lagi ke simpul yang sama tanpa mengulang melewati sisi-sisi (edges) yang sama. Siklus ini penting karena memberikan informasi tentang struktur internal dan pola hubungan dalam sebuah graf.
Siklus dalam graf dibedakan menjadi dua jenis, yaitu siklus sederhana dan siklus Hamilton. Siklus sederhana adalah jalur yang kembali ke simpul asal tanpa melalui simpul lain lebih dari sekali. Sementara itu, siklus Hamilton mengharuskan jalur tersebut mengunjungi setiap simpul tepat satu kali sebelum kembali ke simpul asal.
Penelitian tentang siklus dalam graf memiliki berbagai aplikasi dalam berbagai bidang, seperti dalam ilmu jaringan, komputer, dan penyelesaian masalah logistik. Memahami konsep ini sangatlah penting bagi para peneliti dan praktisi dalam mengembangkan algoritma efisien untuk menyelesaikan masalah-masalah yang melibatkan graf.
Jenis-Jenis Siklus
Dalam teori graf matematika, terdapat beberapa jenis siklus yang sering diidentifikasi dan dipelajari. Masing-masing jenis siklus memiliki karakteristik unik yang membedakan satu sama lain. Berikut adalah beberapa di antaranya:
Siklus Sederhana adalah siklus yang tidak mengulangi sisi-sisi atau simpul-simpul, kecuali pada simpul awal dan akhir yang sama. Siklus ini merupakan bentuk paling dasar dari siklus dalam graf.
Siklus Hamiltonian adalah siklus yang melalui setiap simpul tepat satu kali dan kembali ke simpul awal. Siklus ini dinamai menurut ahli matematika William Rowan Hamilton dan sering digunakan untuk menyelesaikan berbagai masalah optimasi.
Siklus Eulerian ialah siklus yang melalui setiap sisi pada graf tepat satu kali dan kembali ke simpul awal. Siklus ini dinamai sesuai dengan Leonhard Euler, ahli matematika Swiss, yang pertama kali mengembangkan konsep ini.
Siklus Dirac merujuk pada kondisi yang jika setiap simpul dalam graf memiliki degree minimal setengah dari jumlah total simpul, maka graf tersebut memiliki siklus Hamiltonian.
Menganalisis dan mengidentifikasi jenis-jenis siklus ini merupakan bagian penting dalam teori graf karena berdampak pada banyak aplikasi praktis dalam ilmu komputer, jaringan, serta optimasi masalah.
Sifat-Sifat Siklus
Dalam teori graf matematika, siklus memiliki beberapa sifat khas yang membedakannya dari struktur graf lainnya. Salah satu sifat utama siklus adalah bahwa ia merupakan suatu jalan tertutup, di mana titik awal dan titik akhir adalah sama.
Sifat lainnya adalah bahwa dalam siklus, setiap simpul memiliki derajat kedua. Artinya, setiap simpul pada siklus dihubungkan tepat dengan dua sisi. Hal ini memastikan tidak ada simpul yang berdiri sendiri atau berlebihan dalam hubungan.
Selain itu, siklus juga dapat dilabeli sebagai graf hamiltonian jika menyertakan setiap simpul dalam graf tepat satu kali. Hal ini penting dalam memahami perjalanan yang melalui setiap simpul tanpa pengulangan.
Siklus dalam grafik juga memiliki aplikabilitas luas dalam berbagai algoritma dan pemecahan masalah, seperti dalam algoritma siklus Euler yang membantu dalam menemukan perjalanan yang melalui setiap sisi tepat satu kali.
Memahami sifat-sifat siklus membantu para matematikawan dan ilmuwan komputer dalam analisis graf yang lebih mendalam dan akurat. Siklus sering digunakan dalam teori jaringan, pengoptimalan, dan berbagai aplikasi praktis lainnya.
Aplikasi Siklus dalam Graf
Dalam teori graf matematika, siklus memiliki berbagai aplikasi praktis yang sangat penting di berbagai bidang. Salah satu contohnya adalah di bidang komputer, khususnya dalam pengembangan algoritma yang digunakan untuk mendeteksi deadlock dalam sistem operasi.
Siklus dalam graf juga dapat diaplikasikan dalam bidang transportasi, misalnya untuk merencanakan jalur perjalanan yang efektif. Dengan menggunakan graf yang berisi simpul-simpul sebagai titik persinggahan dan ruas sebagai jalan penghubung, kita dapat menentukan siklus mana yang paling optimal untuk menghindari kemacetan atau biaya yang berlebihan.
Selain itu, dalam manajemen jaringan, siklus digunakan untuk mendeteksi dan memperbaiki redundansi dan kerentanan dalam topologi jaringan. Dengan memahami siklus yang ada dalam graf jaringan, kita dapat lebih mudah mengidentifikasi komponen-komponen yang berpotensi menyebabkan kegagalan jaringan.
Penggunaan lain dari siklus dalam graf dapat ditemukan dalam bioinformatika. Analisis siklus dalam graf digunakan untuk memahami interaksi protein dan jalur metabolisme dalam sel. Ini membantu ilmuwan untuk memetakan jaringan biokimia yang kompleks, yang pada akhirnya berkontribusi terhadap penemuan obat baru dan pemahaman yang lebih baik tentang penyakit.