Pemahaman aplikasi matematika dalam fisika merupakan aspek penting dalam memperdalam ilmu pengetahuan. Keterkaitan antara keduanya mencerminkan hubungan erat yang tak terpisahkan. Matematika digunakan sebagai bahasa universal untuk menjelaskan fenomena-fenomena fisika secara kuantitatif. Dengan kata lain, matematika adalah alat yang sangat diperlukan dalam formulasi dan solusi masalah fisika.
Artikel ini akan mengupas lebih dalam mengenai pengertian dari aplikasi matematika dalam fisika. Kami akan membahas bagaimana prinsip-prinsip matematika diterapkan dalam berbagai konsep fisika, seperti mekanika, termodinamika, dan elektrodinamika. Pemahaman lebih dalam tentang topik ini tidak hanya meningkatkan wawasan tetapi juga membantu dalam pengembangan keterampilan analitis yang lebih baik.
Apa itu Aplikasi Matematika dalam Fisika?
Aplikasi matematika dalam fisika merupakan bidang yang mengintegrasikan konsep-konsep matematika untuk memahami dan memecahkan masalah-masalah dalam fisika. Matematika digunakan sebagai alat yang sangat penting untuk menjelaskan fenomena fisik yang kompleks dan abstrak.
Dalam fisika, matematika digunakan untuk membuat model matematis yang menggambarkan sistem atau fenomena alam. Model ini bisa berupa persamaan diferensial, integral, atau bentuk lain dari representasi matematis yang membantu fisikawan dalam memprediksi bagaimana suatu sistem akan bereaksi di bawah kondisi tertentu.
Salah satu contoh aplikasi matematika dalam fisika adalah penggunaan kalkulus dalam mekanika klasik untuk menghitung gerakan benda. Selain itu, aljabar linear juga banyak digunakan dalam fisika kuantum untuk mendeskripsikan keadaan-keadaan sistem kuantum.
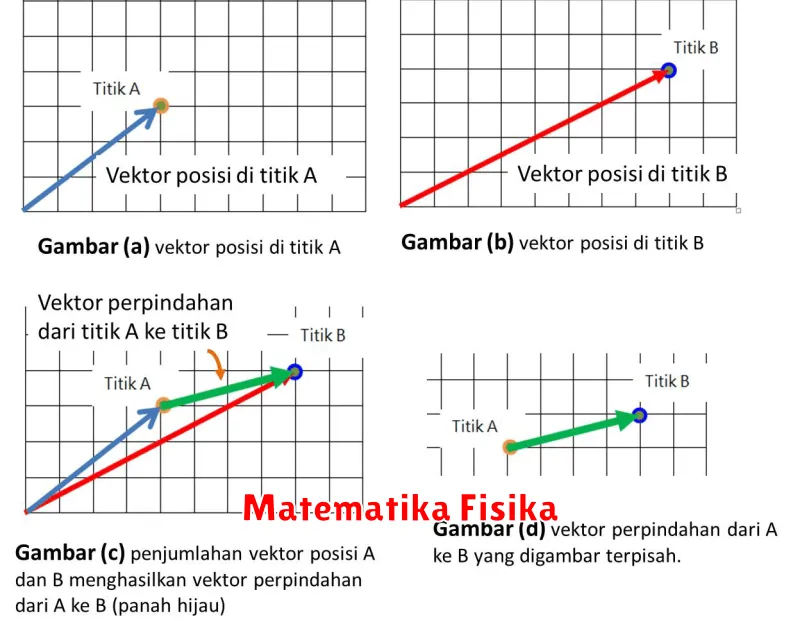
Penggunaan matematika dalam fisika tidak hanya membantu dalam analisis dan prediksi, tetapi juga dalam visualisasi konsep-konsep fisik melalui grafik dan diagram. Ini memungkinkan para ilmuwan untuk mendapatkan pemahaman yang lebih mendalam dan intuitif tentang bagaimana sistem fisik bekerja.
Mengapa Matematika Penting dalam Fisika?
Matematika memainkan peran fundamental dalam perkembangan ilmu fisika. Hal ini disebabkan oleh kemampuannya dalam menyediakan alat untuk mendeskripsikan fenomena alam dengan cara yang presisi dan terukur. Fisika, sebagai ilmu yang mempelajari sifat-sifat dan interaksi materi serta energi, memerlukan kerangka matematika untuk menyusun konsep dan teori yang kompleks.
Salah satu alasan utama mengapa matematika sangat penting dalam fisika adalah karena matematika memungkinkan fisikawan untuk membuat prediksi yang akurat. Dengan menggunakan persamaan matematika, teori fisika dapat diuji dan diverifikasi melalui eksperimen. Sebagai contoh, Hukum Newton dan Teori Relativitas Einstein, yang keduanya bergantung pada prinsip-prinsip matematika untuk dijelaskan dan diverifikasi.
Lebih lanjut, matematika membantu dalam memahami dan menggali fenomena alam yang mungkin tidak dapat dijelaskan hanya dengan pengamatan kualitatif. Konsep-konsep seperti kalkulus, aljabar linier, dan teori grup adalah beberapa alat matematika yang sering digunakan dalam fisika teori untuk memodelkan alam semesta pada tingkat yang mendalam dan kompleks.
Selain itu, matematika juga digunakan dalam pengolahan data dan analisis statistik dalam fisika eksperimental. Dengan bantuan teknik matematika, data yang dihasilkan dari eksperimen fisika dapat dianalisis, diinterpretasikan, dan dimanfaatkan untuk memperkuat atau memodifikasi teori yang ada.
Oleh karena itu, dapat disimpulkan bahwa matematika adalah komponen yang tidak dapat dipisahkan dari fisika. Tanpa adanya matematika, banyak konsep dan teori fisika yang oleh begitu banyak metode penghitungan dan kompleksitas aljabar tidak akan dapat dipahami atau dijelaskan secara memadai. Matematika memberikan bahasa universal yang memungkinkan para ilmuwan untuk mengkomunikasikan dan menguji ide-ide dalam fisika di seluruh dunia.
Contoh Penerapan Matematika dalam Fisika Klasik
Dalam fisika klasik, matematika berperan penting dalam menjelaskan fenomena alam. Salah satu contoh penerapannya adalah dalam hukum Newton tentang gerak. Hukum Newton yang pertama menyatakan bahwa setiap objek akan tetap dalam keadaan diam atau bergerak dengan kecepatan konstan kecuali ada gaya yang bekerja padanya.
Rumus matematika yang digunakan dalam hukum Newton adalah F = ma, di mana F adalah gaya yang bekerja pada objek, m adalah massa objek, dan a adalah percepatan objek tersebut. Dengan menggunakan rumus ini, kita dapat menghitung gaya yang dibutuhkan untuk menggerakkan suatu objek atau memahami bagaimana objek akan bereaksi terhadap gaya tertentu.
Contoh lain penerapan matematika dalam fisika klasik adalah dalam hukum gravitasi universal yang dirumuskan oleh Isaac Newton. Hukum ini menyatakan bahwa setiap dua objek dengan massa akan saling menarik dengan gaya yang besarnya sebanding dengan massa masing-masing objek dan berbanding terbalik dengan kuadrat jarak antara keduanya.
Rumusnya adalah F = G (m1 * m2) / r^2, di mana G adalah konstanta gravitasi universal, m1 dan m2 adalah massa kedua objek, dan r adalah jarak antara kedua objek. Penerapan rumus ini memungkinkan para ilmuwan untuk memprediksi pergerakan planet, bintang, dan objek lainnya dalam tata surya.
Melalui contoh-contoh ini, dapat kita lihat bahwa matematika tidak hanya merupakan alat bantu dalam memecahkan masalah fisika klasik, tetapi juga menjadi fondasi bagi pemahaman kita terhadap alam semesta.
Contoh Penerapan Matematika dalam Fisika Modern
Dalam fisika modern, matematikawan dan fisikawan sering kali bekerja sama untuk memecahkan berbagai masalah yang kompleks. Salah satu contoh penerapan ini adalah dalam teori relativitas yang dikembangkan oleh Albert Einstein. Teori ini menggunakan konsep-konsep matematika lanjutan seperti geometri diferensial dan kalkulus tensor untuk menggambarkan fenomena alam.
Contoh lainnya adalah dalam fisika kuantum, di mana mekanika matriks dan analisis fungsional berperan penting. Fisika kuantum memerlukan pemahaman yang mendalam tentang aljabar linear dan persamaan Schrödinger yang tidak mungkin diselesaikan tanpa matematika tingkat tinggi.
Matematika juga digunakan dalam simulasi komputer yang semakin penting dalam penelitian fisika modern. Algoritma numerik dan metode Monte Carlo adalah dua teknik matematika yang digunakan untuk memodelkan fenomena fisika yang kompleks seperti dinamika fluida dan interaksi partikel pada tingkat sub-atomik.
Selain itu, penerapan teori grup dalam fisika partikel membantu dalam memahami simetri-simetri yang ada di alam semesta. Teori ini membantu dalam pengelompokkan partikel-partikel elementer yang ada dalam Model Standar Fisika Partikel.
Dengan demikian, matematika tidak hanya menjadi alat bantu namun menjadi bahasa utama dalam mengungkapkan konsep-konsep dasar dalam fisika modern. Melalui penerapan ini, banyak fenomena alam dapat dijelaskan secara lebih rinci dan eksak.
Peran Aplikasi Matematika dalam Perkembangan Fisika
Dalam ranah sains, aplikasi matematika memegang peran yang sangat vital, khususnya dalam ilmu fisika. Penerapan konsep matematika seperti kalkulus, aljabar, dan teori himpunan memungkinkan fisikawan untuk mengembangkan dan memahami teori-teori fisika secara mendalam.
Salah satu contoh signifikan adalah penggunaan kalkulus diferensial dan integral dalam memformulasikan hukum-hukum gerak menurut Newton. Dengan bantuan kalkulus, fisikawan dapat menjelaskan pergerakan benda dengan lebih akurat, baik dalam kondisi statis maupun dinamis.
Lebih lanjut, dalam fisika modern, seperti mekanika kuantum dan relativitas umum, matematika berfungsi sebagai dasar utama. Fungsi gelombang dalam mekanika kuantum, yang menggambarkan probabilitas keberadaan partikel, disusun dengan menggunakan persamaan diferensial parsial yang kompleks. Begitu juga, untuk memahami konsep ruang-waktu dalam relativitas umum, diperlukan pemahaman mendalam tentang geometri diferensial dan tensor.
Oleh karena itu, keberadaan matematika tidak hanya membantu dalam perumusan teori-teori baru, tetapi juga dalam melakukan verifikasi eksperimental terhadap teori-teori tersebut. Analisis data eksperimen fisika menggunakan metode statistik dan probabilitas memastikan bahwa hasil yang diperoleh dapat dipertanggungjawabkan secara ilmiah.
Secara keseluruhan, kolaborasi erat antara matematika dan fisika terus mendorong batas-batas pengetahuan manusia dan membuka jalan bagi berbagai inovasi baru dalam teknologi dan teori ilmiah. Sebagai fondasi utama, matematika memungkinkan fisika berkembang dan menjawab pertanyaan-pertanyaan mendasar tentang alam semesta.