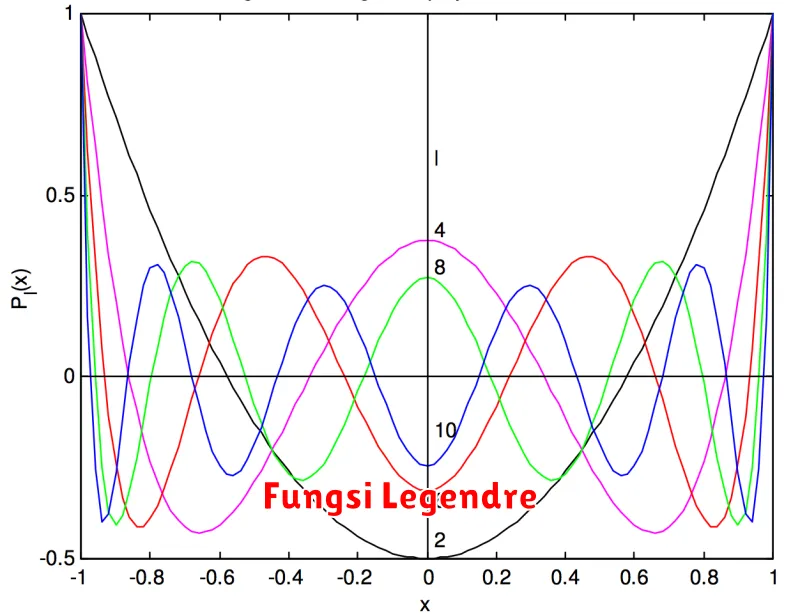
Dalam dunia matematika, terdapat berbagai fungsi yang memiliki peran penting dalam berbagai aplikasi dan teori, salah satunya adalah Fungsi Legendre. Fungsi ini dinamai dari matematikawan Prancis, Adrien-Marie Legendre, yang dikenal atas kontribusinya dalam bidang matematika dan fisika. Artikel ini akan menjelaskan secara mendalam mengenai pengertian Fungsi Legendre dan kegunaannya dalam berbagai disiplin ilmu.
Fungsi Legendre masuk ke dalam kategori fungsi ortogonal, yang sering digunakan dalam teori medan potensial, geofisika, dan elektromagnetisme. Pemahaman yang komprehensif mengenai Fungsi Legendre dapat memberikan wawasan yang lebih luas tentang bagaimana cara kerja sistem-sistem kompleks ini. Oleh karena itu, mempelajari pengertian dan aplikasi dari Fungsi Legendre merupakan langkah penting bagi siapa saja yang tertarik dalam ranah matematika terapan dan fisika teoretis.
Pengertian Fungsi Legendre
Fungsi Legendre adalah solusi dari sebuah diferensial yang digunakan dalam berbagai cabang matematika dan aplikasi fisika. Fungsi ini dinamai sesuai dengan nama matematikawan Prancis, Adrien-Marie Legendre.
Secara umum, Fungsi Legendre muncul dalam persamaan diferensial yang dikenal sebagai Persamaan Legendre. Persamaan ini sering dijumpai dalam konteks masalah yang melibatkan harmonik sferis dan potensial gravitasi.
Dalam bentuk standar, persamaan Legendre didefinisikan sebagai:
(1 – x2) y” – 2xy’ + l(l+1) y = 0
di mana, l adalah bilangan bulat non-negatif, dan y adalah fungsi yang menjadi solusi dari persamaan tersebut.
Solusi dari persamaan ini disebut Polinomial Legendre jika didefinisikan dalam interval [-1, 1]. Dalam beberapa kasus, Fungsi Legendre juga dapat diperluas dalam bentuk yang lebih umum yang dikenal sebagai Fungsi Legendre Asosiasi.
Kegunaan dari Fungsi Legendre tak terhitung dalam berbagai bidang ilmu. Dalam fisika, mereka berguna dalam analisis potensi elektromagnetik serta dalam teori medan kuantum. Sedangkan dalam teknik, mereka membantu dalam memecahkan masalah yang berhubungan dengan stabilitas sistem dinamis.
Dengan segala aplikasinya, memahami Pengertian Fungsi Legendre adalah langkah awal yang penting bagi mereka yang terjun dalam dunia matematika dan fisika terapan. Dengan pemahaman ini, pengembangan lebih lanjut dalam pengetahuan ilmiah dapat dicapai secara lebih mendalam dan komprehensif.
Sifat-sifat Fungsi Legendre
Dalam matematika, Fungsi Legendre memiliki beberapa sifat fundamental yang sangat penting dalam berbagai aplikasi. Sifat-sifat ini termasuk ortogonalitas, hubungan rekursif, serta batas-batas asimtotik.
Ortogonalitas merupakan salah satu sifat kunci dari Fungsi Legendre. Fungsi-fungsi ini ortogonal terhadap satu sama lain dalam interval [-1,1], yang berarti bahwa integral perkalian dua Fungsi Legendre berbeda dalam interval tersebut adalah nol. Hal ini dapat dinyatakan dalam bentuk integral sebagai berikut:
∫ (dari -1 hingga 1) dari Pₙ(x) Pₘ(x) dx = 0, untuk n ≠ m.
Sifat lainnya adalah hubungan rekursif yang memungkinkan komputasi Fungsi Legendre lebih efisien. Fungsi Legendre memenuhi hubungan rekursif yang dinyatakan sebagai:
(n+1)Pₙ₊₁(x) = (2n+1)xPₙ(x) – nPₙ₋₁(x).
Sifat-sifat ini sangat penting untuk aplikasi dalam fisika dan teknik, khususnya dalam penyelesaian persamaan diferensial yang melibatkan masalah batas. Sifat ortogonalitas digunakan dalam metode pemisahan variabel, sedangkan hubungan rekursif memudahkan perhitungan numerik.
Selain itu, Fungsi Legendre juga memiliki sifat batas asimtotik. Dalam kasus batas n yang sangat besar, Fungsi Legendre Pₙ(x) dapat diaproksimasi secara asimtotik yang sangat berguna dalam analisis dan pemrosesan sinyal.
Pemahaman mendalam mengenai sifat-sifat ini memberikan wawasan tambahan dalam menerapkan Fungsi Legendre pada berbagai bidang ilmu, memungkinkan solusi yang lebih efektif dan efisien.
Persamaan Diferensial Fungsi Legendre
Persamaan diferensial fungsi Legendre merupakan salah satu jenis persamaan diferensial yang sering muncul dalam berbagai bidang ilmu, terutama dalam fisika teoretis dan matematika terapan. Persamaan ini dinamakan berdasarkan matematikawan Prancis, Adrien-Marie Legendre, yang mempelajarinya dalam konteks analisis harmonik.
Secara umum, bentuk standar persamaan diferensial Legendre adalah: $$ (1 – x)^2 frac{d^2 y}{dx^2} – 2x frac{d y}{dx} + n(n+1)y = 0 $$ Di mana ( n ) adalah sebuah bilangan bulat yang tidak negatif.
Fungsi-fungsi yang memenuhi persamaan ini disebut sebagai Polinomial Legendre dan diindikasikan dengan ( P_n(x) ). Polinomial-poliminal ini memiliki peran penting dalam teori potensial, pemecahan masalah dalam koordinat bola, dan banyak aplikasi lainnya.
Polinomial Legendre dapat diperoleh dengan metode rekursif atau melalui generating function. Salah satu sifat penting dari polinomial ini adalah ortogonalitasnya dalam interval ([-1, 1]), yang berarti bahwa: $$ int_{-1}^{1} P_m(x) P_n(x) dx = 0 $$ untuk ( m neq n ).
Aplikasi Fungsi Legendre
Fungsi Legendre memiliki berbagai aplikasi dalam disiplin ilmu matematika dan fisika. Fungsi ini sering digunakan dalam teori potensial, khususnya untuk menyelesaikan masalah-masalah yang melibatkan persamaan Laplace dalam koordinat bola.
Dalam fisika kuantum, fungsi Legendre digunakan untuk menggambarkan bentuk orbital atom. Orbital ini dapat dicirikan oleh fungsi harmonik sferis yang merupakan solusi dari persamaan Schrödinger dalam koordinat sferis.
Selain itu, dalam bidang optik, terutama dalam studi tentang optik adaptif, fungsi Legendre digunakan untuk mengoreksi aberasi dalam sistem optik. Fungsi ini membantu dalam pemodelan dan simulasi bentuk lensa yang lebih akurat.
Di bidang teknik elektro, fungsi Legendre juga digunakan dalam analisis spektral untuk menyelesaikan masalah pemfilteran dan dalam komunikasi untuk mengembangkan algoritma pengkodean yang lebih efisien.
Dengan cakupan aplikasi yang luas, fungsi Legendre merupakan alat penting dalam penyelesaian berbagai masalah komputasional dan teoritis dalam ilmu pengetahuan dan teknologi.