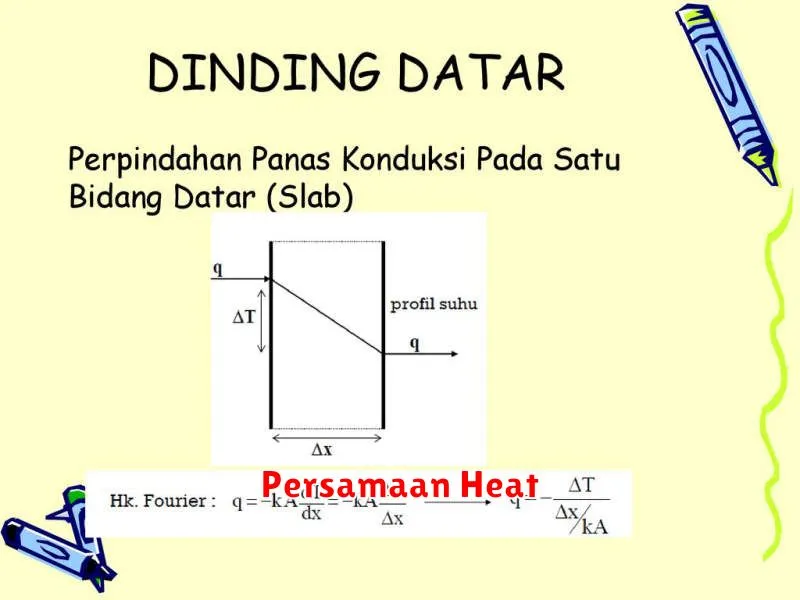
Pada dunia matematika, terdapat berbagai persamaan yang digunakan untuk menggambarkan fenomena alam. Salah satu persamaan yang sangat penting dan sering digunakan adalah persamaan heat. Persamaan ini memiliki peran kunci dalam memahami bagaimana panas atau energi termal menyebar melalui suatu medium, baik itu padat, cair, maupun gas. Oleh karena itu, mempelajari konsep dan aplikasi dari persamaan heat sangat penting bagi ilmuwan, insinyur, dan peneliti yang bekerja di berbagai bidang, dari fisika hingga teknik.
Artikel ini akan mengulas secara mendalam tentang pengertian dan aplikasi dari persamaan heat dalam matematika. Dengan memahami dasar-dasar dan prinsip-prinsip yang mendasari persamaan ini, kita bisa lebih memahami bagaimana panas mengalir dan bagaimana memprediksi perubahan suhu dalam suatu sistem. Pengetahuan ini tidak hanya berguna dalam konteks akademis, tetapi juga dalam aplikasi industri dan berbagai teknologi modern yang kita gunakan sehari-hari.
Apa itu Persamaan Heat?
Persamaan Heat, atau Persamaan Panas, adalah sebuah persamaan diferensial parsial yang digunakan dalam matematika dan fisika untuk memodelkan distribusi panas (atau variasi suhu) dalam suatu benda sepanjang waktu.
Persamaan ini pertama kali diperkenalkan oleh matematikawan Prancis, Joseph Fourier, pada awal abad ke-19. Persamaan ini adalah esensial dalam teori konduksi panas dan banyak digunakan dalam berbagai disiplin ilmu, termasuk teknik, fisika, dan ilmu material.
Secara matematis, persamaan heat dapat dinyatakan dalam bentuk:
Dalam persamaan ini, u(x,t) merepresentasikan suhu pada titik x dan waktu t, sementara α adalah konstanta difusivitas termal yang menunjukkan seberapa cepat panas menyebar melalui medium.
Aplikasi utama dari persamaan heat meliputi analisis masalah pendinginan dan pemanasan, pengendalian proses industri, dan bahkan dalam ilmu lingkungan dan medis.
Bentuk Umum Persamaan Heat
Dalam matematika terapan, persamaan heat sering digunakan untuk memodelkan distribusi panas dalam suatu bahan seiring waktu. Persamaan ini merupakan bagian dari persamaan diferensial parsial, yang menggambarkan bagaimana suhu suatu bahan berubah karena konduksi panas. Bentuk umum dari persamaan heat dalam tiga dimensi adalah:
∂u/∂t = α(∂²u/∂x² + ∂²u/∂y² + ∂²u/∂z²)
Dalam persamaan tersebut, u(x,y,z,t) adalah fungsi suhu yang bergantung pada koordinat ruang (x, y, z) dan waktu (t). Simbol α adalah konstanta difusi termal, yang merupakan properti material yang menentukan seberapa cepat panas menyebar melalui media tersebut.
Penggunaan persamaan ini sangat luas dalam berbagai bidang seperti fisika, teknik, dan keilmuan material untuk memprediksi dan menganalisis penyebaran panas dalam sistem yang berbeda.
Aplikasi Persamaan Heat dalam Ilmu Pengetahuan dan Teknik
Persamaan heat atau heat equation adalah salah satu aspek penting dalam matematika dan aplikasinya sangat luas dalam berbagai bidang ilmu pengetahuan serta teknik. Persamaan ini digunakan untuk menggambarkan distribusi panas atau suhu dalam medium tertentu sebagai fungsi dari waktu dan tempat.
Dalam fisika, persamaan heat memainkan peran kunci dalam studi transfer panas. Contohnya, insinyur sering menggunakan persamaan ini untuk menganalisis aliran panas dalam sistem pendingin mesin atau reaktor nuklir. Dengan memprediksi distribusi suhu, mereka dapat merancang sistem yang lebih efisien dan aman.
Di bidang teknik material, persamaan heat digunakan untuk memahami proses pendinginan atau pemanasan material khususnya dalam proses manufaktur seperti annealing dan quenching. Hal ini membantu dalam menentukan kondisi optimal untuk menghasilkan material dengan sifat mekanik yang diinginkan.
Pada teknik sipil, persamaan heat diterapkan dalam studi konduksi panas di dalam tanah serta dalam desain sistem pemanas dan pendingin untuk bangunan. Pengetahuan ini penting untuk memastikan kenyamanan thermal serta efisiensi energi dalam konstruksi.
Selain itu, dalam bidang ilmiah lain seperti geofisika dan oceanografi, persamaan ini digunakan untuk memahami fenomena alam. Misalnya, konduksi panas dalam mantel bumi atau distribusi suhu di laut yang memengaruhi pola cuaca global.
Metode Penyelesaian Persamaan Heat
Persamaan heat atau heat equation adalah salah satu persamaan diferensial parsial yang sangat penting dalam bidang matematika terapan dan fisika. Persamaan ini digunakan untuk menggambarkan distribusi temperatur (atau variasi panas) dalam suatu benda sepanjang waktu. Memecahkan persamaan ini menuntut teknik dan metode khusus.
Salah satu metode yang populer dalam penyelesaian persamaan heat adalah pemisahan variabel. Metode ini mengasumsikan solusi dapat ditulis sebagai perkalian dari dua fungsi, masing-masing bergantung pada satu variabel saja, misalnya, fungsi yang bergantung pada waktu dan fungsi yang bergantung pada ruang. Langkah pertama adalah mengubah persamaan heat menjadi bentuk yang memungkinkan pemisahan variabel dan kemudian mensubstitusi asumsi solusi tersebut.
Metode lain yang sering digunakan adalah metode transformasi Fourier. Dalam teknik ini, fungsi temperatur diubah menjadi ruang frekuensi menggunakan transformasi Fourier. Kemudian, persamaan diferensial asli diubah menjadi persamaan diferensial biasa yang lebih mudah diatasi. Setelah solusi diperoleh di ruang frekuensi, transformasi Fourier balik digunakan untuk mendapatkan solusi dalam domain asli.
Selain itu, metode numerik seperti metode beda hingga dan elemen hingga juga sangat berguna dalam menyelesaikan persamaan heat terutama untuk kasus dengan kondisi batas kompleks atau geometri tidak standar. Metode ini mendiskretisasi domain serta waktu dan menggunakan algoritma iteratif untuk mendekati solusi.
Penggunaan komputasi terkini dan perangkat lunak matematika seperti MATLAB atau Mathematica sangat membantu dalam implementasi metode-metode ini, memungkinkan penyelesaian yang cepat dan akurat dari masalah yang kompleks.
Contoh Soal dan Pembahasan Persamaan Heat
Pada bagian ini, kami akan membahas contoh soal yang berkaitan dengan persamaan heat dalam matematika. Persamaan heat atau persamaan panas adalah jenis persamaan diferensial parsial yang umum digunakan untuk memodelkan distribusi panas dalam sebuah medium seiring waktu.
Soal: Tentukan solusi dari persamaan heat satu dimensi berikut dengan kondisi awal yang diberikan:
[ u_t = alpha^2 u_{xx}, quad 0<x0, ] dengan kondisi awal [ u(x,0) = f(x), ] dan kondisi batas [ u(0,t)=u(L,t)=0. ]</x
Pembahasan: Untuk menyelesaikan persamaan heat ini, kita dapat menggunakan metode seperation of variables.
1. Pertama, asumsikan solusi dalam bentuk ( u(x,t) = X(x)T(t) ).
2. Substitusi bentuk di atas ke dalam persamaan heat untuk mendapatkan: [ X(x)T'(t) = alpha^2 X”(x)T(t) ]
3. Pisahkan variabel untuk mendapatkan: [ frac{T'(t)}{alpha^2 T(t)} = frac{X”(x)}{X(x)} = -lambda ]
4. Pecahkan dua persamaan diferensial biasa: [ X”(x) + lambda X(x) = 0, ] [ T'(t) + alpha^2lambda T(t) = 0. ]
5. Selanjutnya, selesaikan kondisi batas: [ X(0) = 0 quad dan quad X(L) = 0 ]
6. Solusi dari persamaan ini akan berbentuk: [ X_n(x) = sinleft(frac{npi x}{L}right), quad lambda = left(frac{npi}{L}right)^2, ] [ T_n(t) = e^{-alpha^2left(frac{npi}{L}right)^2 t} ]
7. Jadi solusi umum adalah: [ u(x,t) = sum_{n=1}^{infty} B_n sinleft(frac{npi x}{L}right) e^{-alpha^2left(frac{npi}{L}right)^2 t} ] di mana koefisien ( B_n ) diperoleh dari kondisi awal dengan menggunakan deret Fourier:
[ B_n = frac{2}{L} int_0^L f(x) sinleft(frac{npi x}{L}right) dx ]
Dengan penyelesaian langkah-langkah di atas, kita dapat memperoleh solusi lengkap dari persamaan heat yang diberikan.