Teorema Lagrange merupakan salah satu konsep fundamental dalam matematika yang memiliki banyak aplikasi terutama dalam bidang aljabar dan teori grup. Teorema ini dinamai sesuai dengan nama matematikawan Prancis, Joseph-Louis Lagrange, yang memberikan kontribusi besar dalam pengembangan teori ini. Dalam artikel ini, kita akan mendalami pengertian dan aplikasi dari Teorema Lagrange dalam konteks matematika modern.
Pemahaman yang mendalam mengenai Teorema Lagrange memberikan dasar yang kuat untuk memahami struktur internal dari grup dan subgrup dalam aljabar. Teorema ini menyatakan bahwa order dari setiap subgrup dalam suatu grup adalah pembagi dari order grup tersebut. Pengetahuan mengenai Teorema Lagrange tidak hanya penting bagi para matematikawan, tetapi juga bagi mereka yang terlibat dalam bidang-bidang ilmu pengetahuan yang membutuhkan analisis struktur matematis yang kompleks.
Apa itu Teorema Lagrange?
Teorema Lagrange adalah salah satu teorema penting dalam matematika, khususnya dalam teori grup. Teorema ini dinamai sesuai dengan nama matematikawan Prancis, Joseph-Louis Lagrange, yang memberikan kontribusi signifikan dalam bidang analisis dan teori angka.
Secara formal, teorema ini menyatakan bahwa dalam sebuah grup berhingga, ordo (order) dari setiap subgrup membagi ordo grup tersebut dengan tepat. Ini berarti bahwa jika kita memiliki sebuah grup ( G ) dengan ordo ( |G| ), dan ( H ) adalah subgrup dari ( G ) dengan ordo ( |H| ), maka ( |H| ) adalah pembagi dari ( |G| ).
Dengan kata lain, ini juga bisa dituliskan sebagai ( |G| = |H| cdot k ) untuk beberapa bilangan bulat ( k ). Teorema ini memberikan wawasan penting bagi struktur internal dari grup berhingga dan sangat berperan dalam perkembangan teori grup.
Aplikasi dari Teorema Lagrange dapat ditemukan dalam berbagai bidang matematis, termasuk dalam menyelesaikan persamaan polinomial dan dalam algoritma kriptografi.
Rumus Teorema Lagrange
Teorema Lagrange, atau yang dikenal juga dengan Teorema Nilai Rata-rata, merupakan salah satu konsep penting dalam analisis matematika. Teorema ini menyatakan bahwa untuk setiap fungsi kontinu yang dapat dikalkulasi pada interval tertutup [a, b] dan terdiferensiasi pada interval terbuka (a, b), ada setidaknya satu titik c di antara a dan b yang memenuhi kondisi tertentu.
Secara matematis, Teorema Lagrange dapat dinyatakan dengan rumus berikut:
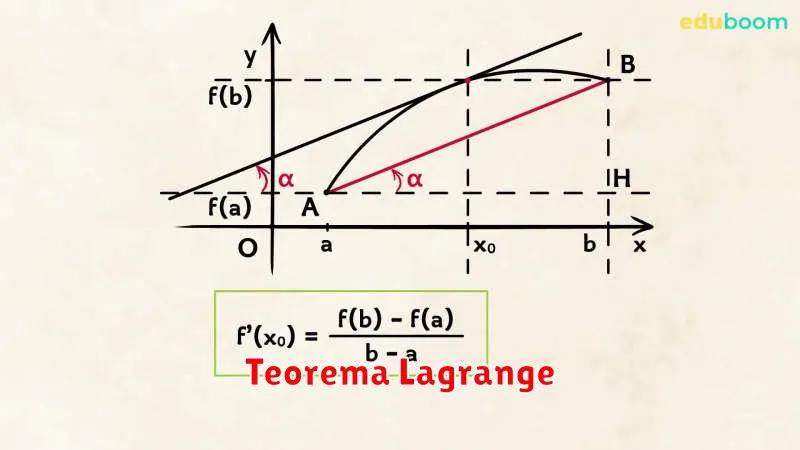
f'(c) = (f(b) – f(a)) / (b – a)
Dalam rumus tersebut, f'(c) merupakan turunan pertama dari fungsi f di titik c, sedangkan f(a) dan f(b) adalah nilai fungsi f di titik a dan b. Rumus ini menunjukkan bahwa pada titik c, kemiringan garis sekan yang menghubungkan titik (a, f(a)) dan (b, f(b)) sama dengan turunan dari fungsi f di titik c.
Persyaratan utama yang harus dipenuhi agar rumus ini berlaku adalah bahwa fungsi f harus kontinu pada interval tertutup dan terdiferensiasi pada interval terbuka. Ini memastikan bahwa ada nilai titik c yang berada di antara a dan b yang memenuhi persamaan tersebut.
Teorema ini memainkan peran penting dalam berbagai aplikasi matematika, baik dalam bidang teori maupun praktis. Oleh karena itu, pemahaman yang baik tentang rumus Teorema Lagrange sangat esensial bagi siapa pun yang mempelajari matematika secara mendalam.
Syarat Penggunaan Teorema Lagrange
Untuk menggunakan Teorema Lagrange dalam matematika, ada beberapa syarat yang harus dipenuhi. Pertama, fungsi yang akan dianalisis harus merupakan fungsi kontinu pada interval tertutup [a, b]. Kontinuitas ini memastikan bahwa fungsi tidak memiliki ketidakpastian atau diskontinuitas pada interval tersebut.
Syarat kedua adalah fungsi tersebut harus diferensial pada interval terbuka (a, b). Artinya, turunan fungsi harus ada dan terdefinisi dengan baik di setiap titik dalam interval ini. Jika fungsi tidak diferensial pada beberapa titik di interval terbuka, maka Teorema Lagrange tidak dapat diterapkan.
Terakhir, terdapat dua titik ekstrim nilai batas, yakni f(a) dan f(b), di mana a dan b adalah batas interval. Nilai dari fungsi pada kedua titik ini menjadi dasar untuk mencari nilai c dalam interval (a, b) yang sesuai dengan syarat dari Teorema Lagrange, yaitu bahwa f'(c) = (f(b) – f(a)) / (b – a).
Interpretasi Geometris Teorema Lagrange
Teorema Lagrange menyatakan bahwa jika fungsi kontinu dan diferensial f(x) pada interval tertutup [a, b], maka terdapat setidaknya satu titik c di dalam interval (a, b) di mana turunan pertama fungsi tersebut sama dengan kemiringan garis yang menghubungkan dua titik akhir interval tersebut yaitu (f(b) – f(a)) / (b – a). Interpretasi geometris ini memberikan pandangan bahwa ada suatu titik di grafik fungsi di mana kemiringan tangen lokal sama dengan kemiringan garis secant.
Dalam konteks geometris, teorema ini dapat divisualisasikan dengan menggambar grafik suatu fungsi pada interval [a, b]. Garis secant yang menghubungkan titik (a, f(a)) dan (b, f(b)) memiliki kemiringan tertentu. Teorema Lagrange menyatakan bahwa ada minimal satu titik c di mana kemiringan garis tangen pada grafik di titik c tersebut sama dengan kemiringan garis secant. Visualisasi ini memperkuat konsep bahwa perubahan rata-rata pada interval [a, b] selalu dapat ditemukan pada suatu titik spesifik di dalam interval tersebut.
Dengan memahami interpretasi geometris dari teorema Lagrange, kita dapat lebih mudah menganalisis perilaku fungsi dalam interval tertentu dan menentukan titik-titik penting yang relevan untuk banyak aplikasi dalam studi matematika maupun sains lain. Sebagai contoh, dalam fisika, teorema ini membantu memahami kecepatan rata-rata dan percepatan.
Aplikasi Teorema Lagrange dalam Kalkulus
Teorema Lagrange atau yang juga dikenal sebagai Teorema Nilai Rata-rata dalam kalkulus, memiliki aplikasi yang luas dalam berbagai bidang. Teorema ini menyatakan bahwa jika sebuah fungsi kontinu pada interval tertutup dan terdiferensialkan pada interval terbuka, maka terdapat setidaknya satu titik dalam interval tersebut di mana turunan fungsi sama dengan rata-rata perubahan fungsi pada interval.
Salah satu aplikasi utama Teorema Lagrange adalah dalam analisis fungsi. Dengan menggunakan teorema ini, kita bisa menentukan bahwa jika turunan pertama dari suatu fungsi konstan, maka fungsi tersebut berupa garis lurus. Ini sangat penting dalam menemukan sifat-sifat fungsi tersebut dan membantu dalam menyelesaikan berbagai masalah dalam kalkulus.
Teorema ini juga digunakan dalam optimalisasi fungsi. Dalam berbagai masalah ekonomi, fisika, dan teknik, optimalisasi menjadi masalah yang sering dibahas. Dengan menerapkan Teorema Lagrange, kita dapat menemukan titik maksimum atau minimum dari suatu fungsi, yang sangat berguna dalam menentukan nilai optimal dari suatu proses atau sistem.
Selain itu, Teorema Lagrange sering diterapkan dalam mengukur kesalahan aproksimasi. Dalam metode numerik, kesalahan aproksimasi sering harus diminimalkan untuk mendapatkan hasil yang lebih akurat. Teorema ini memberikan cara untuk memperkirakan besaran kesalahan tersebut.
Secara lebih luas, Teorema Lagrange juga dapat digunakan dalam analisis kecepatan dan percepatan dalam fisika. Misalnya, dalam menentukan laju perubahan kecepatan sebuah objek dalam interval waktu tertentu, aplikasi teorema ini dapat memberikan estimasi yang akurat.
Dengan demikian, Teorema Lagrange memainkan peran yang sangat penting dalam berbagai aplikasi praktis, baik dalam ilmu pengetahuan maupun dalam masalah sehari-hari yang memerlukan perhitungan dan analisis kalkulus yang mendalam.
Aplikasi Teorema Lagrange dalam Kehidupan Nyata
Teorema Lagrange merupakan salah satu konsep penting dalam matematika yang memiliki aplikasi luas dalam berbagai bidang kehidupan. Salah satu contoh penerapannya yang terkenal adalah dalam optimasi. Di sektor bisnis dan industri, teorema ini digunakan untuk meningkatkan efisiensi proses produksi dengan meminimalkan biaya dan memaksimalkan output.
Selain itu, teorema Lagrange juga berperan penting dalam ilmu teknik. Dalam perancangan struktur dan mekanika, teorema ini membantu insinyur untuk menentukan titik-titik kritis dan memastikan bahwa struktur yang dibuat dapat menahan beban yang diharapkan tanpa membahayakan.
Sebagai tambahan, di bidang ekonomi, teorema ini memberikan kontribusi dalam analisis keseimbangan pasar. Dengan menggunakan teorema Lagrange, para ekonom dapat mengevaluasi kondisi optimal dalam distribusi sumber daya serta penetapan harga dalam pasar kompetitif.
Penerapan lainnya adalah dalam bidang fisika, khususnya mekanika klasik dan kuantum. Teorema ini digunakan untuk menyederhanakan dan memecahkan persamaan gerak, membantu ilmuwan memahami dinamika sistem fisik dengan lebih tepat dan efisien.
Contoh Soal dan Pembahasan Teorema Lagrange
Teorema Lagrange adalah salah satu teorema fundamental dalam kalkulus yang menyatakan bahwa jika suatu fungsi f kontinu di interval [a, b] dan terdiferensialkan di interval (a, b), maka terdapat sebuah titik c di dalam interval (a, b) yang memenuhi:
f'(c) = (f(b) – f(a)) / (b – a)
Untuk lebih memahami penerapan Teorema Lagrange, mari kita bahas contoh soal berikut:
Contoh Soal: Diketahui fungsi f(x) = x^2 + 2x + 1. Tentukan titik c di interval [1, 3] yang memenuhi teorema Lagrange.
Pembahasan:
Pertama, kita perlu memeriksa apakah fungsi f memenuhi syarat-syarat Teorema Lagrange. Fungsi f adalah sebuah polinomial, sehingga ia kontinu dan terdiferensialkan di seluruh bilangan real.
Kemudian, kita hitung nilai f di ujung-ujung interval:
f(1) = 1^2 + 2*1 + 1 = 4
f(3) = 3^2 + 2*3 + 1 = 16
Karena f kontinu di [1, 3] dan terdiferensialkan di (1, 3), oleh Teorema Lagrange, ada titik c di (1, 3) yang memenuhi:
f'(c) = (f(3) – f(1)) / (3 – 1)
f'(x) = 2x + 2
Jadi kita harus menemukan c yang memenuhi:
2c + 2 = (16 – 4) / 2
2c + 2 = 6
2c = 4
c = 2
Maka titik c yang memenuhi teorema Lagrange untuk fungsi dan interval yang diberikan adalah c = 2.