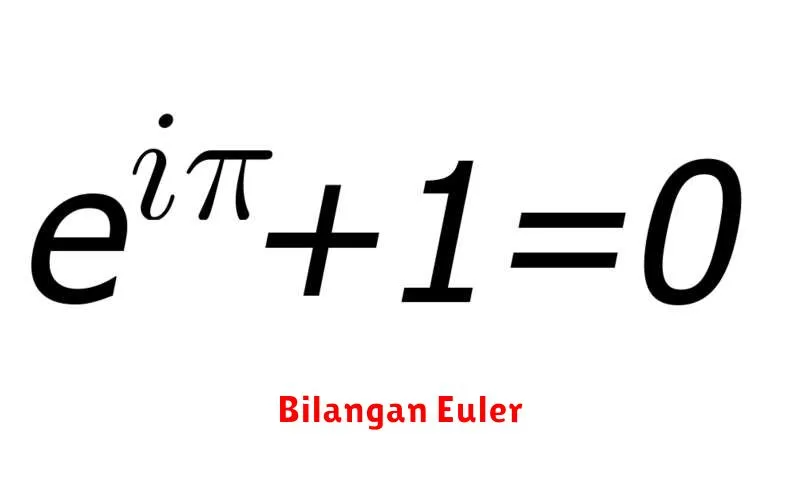Dalam dunia matematika, terdapat banyak konstanta yang memegang peranan penting dalam membantu kita memahami berbagai konsep. Salah satu konstanta yang memiliki keistimewaan tersendiri adalah Bilangan Euler. Dikenal dengan simbol e, bilangan ini sering kali dianggap sebagai salah satu misteri yang menakjubkan dalam ilmu matematika. Artikel ini akan mengulas lebih dalam mengenai asal usul, properti, dan aplikasi dari konstanta yang fenomenal ini.
Penggunaan bilangan Euler tidak hanya terbatas pada matematika murni, tetapi juga memiliki implikasi yang luas dalam bidang sains dan teknik. Mulai dari kalkulus hingga fisika kuantum, bilangan ini muncul dalam berbagai rumus dan persamaan yang rumit. Dengan memahami bilangan Euler, kita dapat lebih menghargai keindahan dan kompleksitas dari dunia matematika yang sering kali tersembunyi di balik angka-angka dan simbol-simbol matematis. Jadi, mari kita jelajahi lebih dalam tentang bilangan yang mengagumkan ini dan lihat bagaimana ia menjadi kunci untuk membuka berbagai rahasia alam semesta.
Pengantar Bilangan Euler
Bilangan Euler, yang sering disimbolkan sebagai e, adalah salah satu konstanta paling penting dalam matematika. Nilainya mendekati 2.71828 dan memiliki peran kunci dalam berbagai cabang ilmu matematika, seperti analisis dan teori bilangan.
Nama bilangan ini diambil dari seorang ahli matematika Swiss bernama Leonhard Euler yang banyak berkontribusi dalam pengembangannya pada abad ke-18. Namun, akar dari konsep ini sebenarnya sudah dimulai oleh Jacob Bernoulli yang mempelajari bunga majemuk, sebuah proses yang menunjukkan pertumbuhan eksponensial.
Bilangan Euler memiliki banyak sifat matematis yang unik. Salah satunya adalah perannya dalam deret eksponensial, yaitu ekspansi Taylor dari fungsi eksponensial. Dalam bentuk persamaan, ini dapat dinyatakan sebagai:
e^x = 1 + x + x^2/2! + x^3/3! + ...
Salah satu aplikasi signifikan dari bilangan Euler adalah dalam kalkulus, khususnya dalam konsep derivatif dan integral yang melibatkan fungsi eksponensial. Selain itu, bilangan ini juga muncul dalam berbagai persamaan diferensial dan memiliki relevansi dalam fisika serta ilmu ekonomi.
Memahami bilangan Euler bukan hanya penting untuk aplikasi praktis, tetapi juga memberikan wawasan mendalam tentang sifat dasar dari matematika itu sendiri. Kesederhanaan dan kecantikan dari konstanta ini seringkali membuatnya menjadi topik yang penuh dengan misteri dan kekaguman bagi para matematikawan dan ilmuwan.
Definisi Bilangan Euler
Bilangan Euler, yang sering kali dilambangkan dengan huruf e, merupakan salah satu konstanta matematika yang fundamental dan sangat penting dalam berbagai disiplin ilmu, terutama dalam kalkulus dan analisis matematika. Nilainya kira-kira sekitar 2.71828, yang merupakan basis dari logaritma alami.
Bilangan ini pertama kali diidentifikasi oleh matematikawan asal Swiss, Leonhard Euler, pada abad ke-18. Matematika kontinental, terutama dalam konteks deret tak berhingga, sering memanfaatkan konstanta ini. Bilangan e muncul dalam berbagai situasi alamiah dan keuangan, seperti dalam pemodelan pertumbuhan eksponensial dan perhitungan bunga majemuk.
Bilangan Euler juga memiliki sifat-sifat unik yang membuatnya istimewa dalam matematika. Salah satu sifat utama adalah bahwa e adalah satu-satunya bilangan riil yang memiliki turunan yang sama dengan nilainya sendiri. Ini berarti jika kita memiliki fungsi eksponensial dengan basis e, turunan dari fungsi tersebut akan tetap sama dengan fungsi aslinya.
Euler’s Number dapat ditemukan dalam rumus Euler yang terkenal: eiπ + 1 = 0, yang menghubungkan lima konstanta matematika utama dalam satu persamaan yang elegan dan memukau secara estetika.
Sifat-sifat Unik Bilangan Euler
Bilangan Euler, yang sering dilambangkan dengan huruf e, memiliki beberapa sifat unik yang menjadikannya salah satu konstanta matematika paling penting dalam berbagai disiplin ilmu. Salah satu sifat utamanya adalah bahwa bilangan ini merupakan pangkat dasar dari logaritma alami. Dengan kata lain, logaritma alami dari e adalah 1, yaitu ln(e) = 1.
Sifat penting lainnya adalah bahwa bilangan Euler dapat diekspresikan sebagai deret takhingga, yaitu e = 1 + 1/1! + 1/2! + 1/3! + 1/4! + …. Deret ini menunjukkan bagaimana e dapat dihitung dengan presisi yang semakin meningkat dengan menambah jumlah suku dalam deret tersebut. Hal ini memberikan dasar bagi pengembangan lebih lanjut dalam analisis matematika dan kalkulus.
Bilangan Euler juga memiliki peranan penting dalam fungsi eksponensial. Fungsi eksponensial berinisialkan ex memiliki sifat eksponensial yang unik, seperti identitas Euler yang terkenal, yaitu eiπ + 1 = 0. Identitas ini menghubungkan lima bilangan fundamental dalam matematika: e, π, i (unit imajiner), 1, dan 0.
Dalam dunia keuangan, bilangan Euler digunakan dalam perhitungan bunga majemuk. Formula ini menyatakan bahwa bunga yang diakumulasi terus-menerus pada tingkat suku bunga tahunan r adalah P(1 + r/n)nt, dan ketika n mendekati takhingga, rumus tersebut mendekati Pert. Hal ini menunjukkan pentingnya e dalam aplikasi praktis di luar matematika murni.
Dengan berbagai sifat unik yang dimilikinya, bilangan Euler tidak hanya menjadi pusat perhatian dalam studi matematika, tetapi juga memberikan kontribusi besar dalam aplikasi praktis di berbagai bidang ilmu pengetahuan, termasuk fisika, keuangan, dan teknik.
Kalkulus dan Bilangan Euler
Bilangan Euler, yang dilambangkan sebagai e, merupakan salah satu konstanta paling penting dalam dunia matematika, khususnya dalam bidang kalkulus. Bilangan ini diperkenalkan oleh Leonhard Euler pada abad ke-18. Nilai e adalah sekitar 2.71828 dan memiliki sifat yang luar biasa dalam berbagai aspek matematika.
Salah satu keterkaitan kuat antara bilangan Euler dan kalkulus adalah melalui konsep fungsi eksponensial. Fungsi eksponensial yang berbasis pada bilangan e, yaitu ex, memiliki sifat unik di mana turunannya adalah fungsi itu sendiri. Hal ini membuat fungsi eksponensial sangat bermanfaat dalam menyelesaikan persamaan diferensial, yang merupakan salah satu topik sentral dalam kalkulus.
Bilangan Euler juga muncul dalam limit terkenal yang mendefinisikan e, yaitu:
e = lim (n → ∞) (1 + 1/n)n
Limit ini menggambarkan pertumbuhan eksponensial dan merupakan dasar dari banyak konsep dalam kalkulus integral dan turunan.
Selain itu, bilangan e sangat penting dalam teori peluang dan statistik, terutama dalam distribusi normal. Fungsi densitas dari distribusi normal melibatkan bilangan e, yang menunjukkan seberapa dalam konstanta ini tertanam dalam berbagai bidang matematika.
Pemahaman mendalam tentang bilangan Euler memberikan wawasan lebih dalam tentang perilaku fungsi dan fenomena alam yang bersifat eksponensial. Oleh karena itu, bilangan e bukan hanya sebatas konstanta matematika, tetapi juga kunci untuk memahami banyak aspek dalam kalkulus dan penerapannya di dunia nyata.
Penggunaan Bilangan Euler di Berbagai Bidang
Bilangan Euler, yang dikenal dengan simbol e, merupakan salah satu konstanta matematika yang paling penting dan memiliki aplikasi luas di berbagai bidang. Dalam matematika, bilangan e sering muncul dalam kajian limit, deret tak hingga, dan fungsi eksponensial, menjadikannya alat yang sangat esensial dalam analisis matematika.
Dalam fisika, bilangan e digunakan untuk menggambarkan proses yang melibatkan pertumbuhan eksponensial atau peluruhan eksponensial. Contohnya, dalam studi radioaktivitas, peluruhan eksponensial material radioaktif sering kali digambarkan dengan menggunakan eksponen bilangan Euler.
Bidang keuangan juga tidak luput dari penggunaan bilangan Euler. Dalam perhitungan bunga majemuk, formula yang melibatkan e membantu dalam memperkirakan nilai masa depan investasi dengan lebih akurat. Hal ini memberikan wawasan yang lebih baik untuk kondisi pasar dan keputusan investasi.
Dalam teknologi informasi dan kriptografi, bilangan Euler menjadi dasar untuk beberapa algoritma enkripsi yang canggih. Misalnya, algoritma RSA yang digunakan untuk komunikasi aman di internet, bergantung pada sifat-sifat bilangan e untuk enkripsi dan dekripsi data.
Bidang biologi dan ilmu kedokteran juga merasakan manfaat dari konstanta ini. Model pertumbuhan populasi mikroorganisme atau penyebaran penyakit sering menggunakan fungsi eksponensial dengan bilangan e untuk menggambarkan peningkatan atau penurunan jumlah organisme atau individu yang terinfeksi.
Dalam seni dan arsitektur, konstanta e dikenal sebagai bagian dari prinsip-prinsip desain yang melibatkan rasio emas dan elemen-elemen simetri dalam struktur yang kompleks. Penggunaan ini menekankan keindahan dan harmonisasi yang matematis dalam seni visual dan bangunan.
Secara keseluruhan, penerapan bilangan Euler dalam berbagai bidang menunjukkan betapa luas dan pentingnya konstanta ini dalam sains, teknologi, dan kehidupan sehari-hari.
Contoh Soal dan Aplikasi
Bilangan Euler, dilambangkan sebagai e, adalah salah satu konstanta paling penting dalam matematika. Salah satu karakteristik utama dari bilangan ini adalah bahwa ia sering muncul dalam berbagai bidang mulai dari kalkulus, ke teori bilangan, hingga statistik.
Untuk memahami aplikasi praktis dari bilangan Euler, berikut adalah beberapa contoh soal yang relevan:
Contoh Soal 1: Hitunglah nilai dari ekspresi berikut: ( e^1 times e^2 ).
Penyelesaian: Menggunakan sifat eksponensial ( e^{a} times e^{b} = e^{a+b} ), maka ( e^1 times e^2 = e^{1+2} = e^3 ).
Contoh Soal 2: Misalkan fungsi eksponensial ( f(x) = e^x ), temukan turunan pertama dari fungsi tersebut.
Penyelesaian: Turunan dari ( f(x) = e^x ) adalah ( f'(x) = e^x ). Ini salah satu sifat unik dari fungsi eksponensial dengan basis e.
Selain dalam soal-soal di atas, bilangan Euler memiliki aplikasi nyata dalam kehidupan sehari-hari. Contohnya adalah dalam bidang ekonomi dan finansial, bilangan Euler digunakan dalam perhitungan bunga majemuk. Bunga majemuk dihitung menggunakan rumus ( A = P left(1 + frac{r}{n}right)^{nt} ), yang mendekati bentuk eksponensial ( A = Pe^{rt} ) ketika jumlah periode penggantian bunga ( n ) menjadi sangat besar.
Contoh lain dari aplikasi bilangan Euler adalah dalam teori probabilitas, khususnya dalam distribusi eksponensial dan distribusi Poisson. Distribusi eksponensial sering muncul dalam analisis waktu antara kedatangan peristiwa, sedangkan distribusi Poisson digunakan untuk mengukur jumlah kemunculan kejadian tertentu dalam interval waktu tertentu.