Dalam dunia matematika, salah satu cabang ilmu yang memiliki daya tarik tersendiri serta menyimpan banyak misteri adalah trigonometri. Trigonometri tidak hanya berperan penting dalam menyelesaikan berbagai permasalahan yang melibatkan segitiga, tetapi juga digunakan dalam berbagai penerapan di bidang lain, seperti fisika, astronomi, dan teknik. Artikel ini bertujuan untuk menguak misteri di balik konsep dasar trigonometri serta bagaimana penerapannya dalam kehidupan sehari-hari.
Dengan memahami konsep dasar trigonometri, kita dapat lebih mudah menyelesaikan berbagai soal dan problematika yang muncul. Tidak hanya sebatas pada sudut dan segitiga, namun trigonometri juga memungkinkan kita untuk menjelajahi fenomena alam yang kompleks dengan mudah dan akurat. Mari kita bersama-sama mempelajari apa itu trigonometri, bagaimana ia bekerja, serta penerapannya dalam berbagai bidang ilmu pengetahuan sehingga mampu memberikan dampak signifikan dalam kehidupan modern saat ini.
Apa Itu Trigonometri?
Trigonometri adalah salah satu cabang ilmu matematika yang mempelajari hubungan antara sudut dan sisi dalam suatu segitiga. Istilah ini berasal dari bahasa Yunani, yaitu dari kata “trigonon” yang berarti segitiga, dan “metron” yang berarti mengukur.
Pada dasarnya, trigonometri adalah ilmu yang sangat penting dalam berbagai bidang, mulai dari fisika, teknik, astronomi, hingga geodesi. Trigonometri membantu kita memahami dan menghitung panjang sisi serta besar sudut dalam sebuah segitiga, baik pada segitiga siku-siku maupun segitiga sembarang.
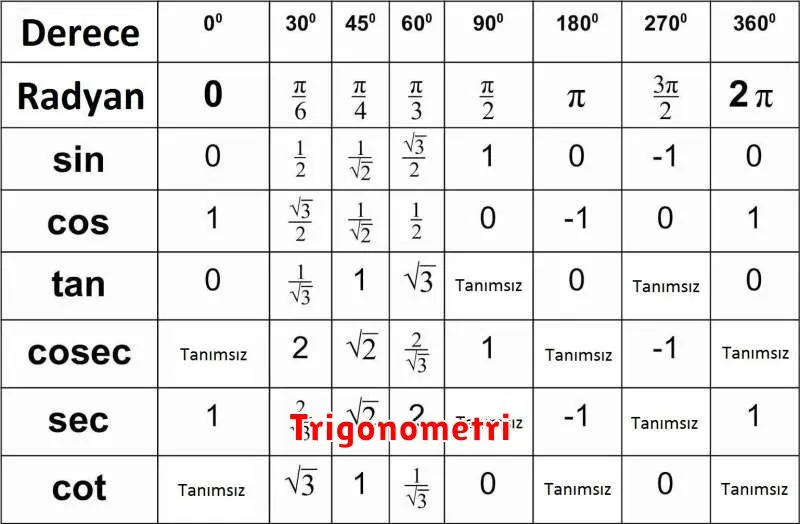
Salah satu konsep fundamental dalam trigonometri adalah penggunaan fungsi trigonometri seperti sine (sin), cosine (cos), dan tangent (tan). Fungsi-fungsi ini menghubungkan sudut dalam segitiga dengan proporsi tertentu dari sisi-sisinya, yang kemudian mempermudah dalam menyelesaikan berbagai masalah geometris.
Segitiga Siku-Siku: Pondasi Trigonometri
Segitiga siku-siku adalah jenis segitiga yang memiliki satu sudut 90 derajat. Dalam bidang trigonometri, segitiga ini memegang peranan penting sebagai pondasi untuk memahami konsep dasar seperti sinus, kosinus, dan tangen.
Pada segitiga siku-siku, panjang setiap sisi memiliki hubungan yang erat dengan sudut-sudut di dalamnya. Sisi terpanjang, yang berhadapan langsung dengan sudut siku-siku, disebut hipotenusa. Sementara itu, dua sisi lainnya dikenal sebagai kaki-kaki segitiga.
Konsep sinus dalam trigonometri didefinisikan sebagai perbandingan antara panjang sisi depan dengan panjang sisi miring (hipotenusa). Secara matematis, ditulis sebagai sin(θ) = depan / hipotenusa. Begitu pula, kosinus adalah perbandingan antara panjang sisi samping dengan hipotenusa, dinyatakan dalam rumusan cos(θ) = samping / hipotenusa. Sedangkan tangen dinyatakan sebagai hasil bagi antara panjang sisi depan dan panjang sisi samping, atau tan(θ) = depan / samping.
Pemahaman mengenai fungsi-fungsi trigonometri yang tercipta dari segitiga siku-siku ini sangat penting dalam berbagai cabang matematika dan ilmu pengetahuan lainnya. Aplikasi dari fungsi-fungsi ini sangat luas, mulai dari pemecahan masalah geometri, fisika, hingga teknik.
Fungsi Trigonometri Dasar: Sinus, Cosinus, dan Tangen
Dalam dunia matematika, fungsi trigonometri memainkan peran penting dalam memahami hubungan antara sudut dan sisi dalam segitiga. Tiga fungsi trigonometri dasar yang sering digunakan adalah sinus, cosinus, dan tangen. Fungsi ini sangat penting terutama dalam bidang geometri, kalkulus, dan analisis matematika lainnya.
Sinus (sin) adalah rasio antara panjang sisi yang berhadapan dengan sudut tertentu terhadap panjang hipotenusa dalam segitiga siku-siku. Secara matematis, dapat ditulis sebagai:
sin θ = (sisi berhadapan) / (hipotenusa).
Cosinus (cos) adalah rasio antara panjang sisi yang bersebelahan dengan sudut tertentu terhadap panjang hipotenusa. Formula untuk menghitung cosinus adalah:
cos θ = (sisi bersebelahan) / (hipotenusa).
Tangen (tan) adalah rasio antara panjang sisi yang berhadapan dengan sudut tertentu terhadap panjang sisi yang bersebelahan. Tangen dapat ditulis sebagai:
tan θ = (sisi berhadapan) / (sisi bersebelahan).
Ketiga fungsi ini memiliki kegunaan dan aplikasi yang luas dalam berbagai disiplin ilmu. Dari perhitungan ketinggian bangunan hingga grafik dan analisis gelombang, sinus, cosinus, dan tangen merupakan dasar dari pemahaman trigonometri yang lebih kompleks.
Menghitung Sudut dan Sisi Segitiga dengan Trigonometri
Trigonometri merupakan cabang matematika yang mempelajari hubungan antara panjang sisi dan besar sudut dalam sebuah segitiga. Dalam konteks ini, pemahaman konsep dasar trigonometri sangat penting guna menghitung sudut dan sisi segitiga secara akurat.
Pada segitiga siku-siku, terdapat tiga fungsi trigonometri utama yang sering digunakan, yaitu sine (sin), cosine (cos), dan tangent (tan). Fungsi-fungsi ini memiliki peran krusial dalam menentukan panjang sisi atau besar sudut segitiga berdasarkan informasi yang sudah diketahui.
Mari kita tinjau penggunaan ketiga fungsi ini dalam menghitung sudut dan sisi segitiga:
- Sine (sin): Sin θ = panjang sisi depan sudut / panjang sisi miring (hipotenusa)
- Cosine (cos): Cos θ = panjang sisi samping sudut / panjang sisi miring (hipotenusa)
- Tangent (tan): Tan θ = panjang sisi depan sudut / panjang sisi samping sudut
Dengan menggunakan fungsi-fungsi ini, kita dapat menentukan panjang sisi yang belum diketahui maupun sudut yang belum diketahui dalam sebuah segitiga. Sebagai contoh, jika diketahui panjang sisi depan dan samping, kita bisa menghitung sudut menggunakan fungsi tangent:
θ = arctan(panjang sisi depan / panjang sisi samping)
Begitu pula dengan sisi miring yang dapat dihitung menggunakan fungsi sine atau cosine, bergantung pada panjang sisi yang diketahui:
- Sisi Miring = panjang sisi depan / sin θ
- Sisi Miring = panjang sisi samping / cos θ
Dengan pemahaman dan penerapan konsep ini, trigonometri menjadi alat yang sangat efektif dalam berbagai situasi matematika dan sains. Penggunaan trigonometri tidak terbatas hanya pada segitiga siku-siku, tetapi juga pada segitiga sembarang dengan bantuan hukum sinus dan hukum cosinus.
Aplikasi Trigonometri dalam Kehidupan Sehari-hari
Trigonometri, salah satu cabang dari matematika, tidak hanya bermanfaat dalam teori namun juga memiliki banyak aplikasi praktis dalam kehidupan sehari-hari. Konsep dasar trigonometri sering digunakan untuk memecahkan berbagai masalah di berbagai bidang seperti arsitektur, astronomi, dan teknik.
Salah satu aplikasi paling umum dari trigonometri adalah dalam bidang konstruksi dan arsitektur. Para insinyur dan arsitek menggunakan prinsip-prinsip trigonometri untuk menghitung dimensi bangunan, sudut kemiringan atap, serta memastikan stabilitas struktur bangunan.
Selain itu, trigonometri juga sangat penting dalam navigasi dan geografi. Misalnya, navigasi maritim dan penerbangan mengandalkan trigonometri untuk menentukan posisi kapal atau pesawat di laut lepas atau udara. Teknik triangulasi, yang menggunakan konsep-konsep trigonometri, memungkinkan penentuan lokasi dengan akurasi tinggi.
Di bidang astronomi, trigonometri digunakan untuk mengukur jarak antara bintang dan planet. Dengan mengetahui sudut dan jarak beberapa titik referensi, para ilmuwan dapat menghitung jarak yang sangat jauh di luar angkasa.
Trigonometri juga diterapkan dalam bidang teknologi sehari-hari, seperti dalam desain dan pengembangan perangkat elektronik yang memerlukan pemahaman tentang gelombang dan sinyal. Misalnya, dalam pengolahan sinyal digital, konsep sinus dan cosinus digunakan untuk merancang filter dan pemroses sinyal.
Penggunaan trigonometri bahkan dapat ditemui dalam bidang kesehatan. Misalnya, dalam radiologi, trigonometri digunakan untuk menentukan sudut optimal dalam pencitraan medis untuk mendapatkan hasil yang paling akurat.
Dengan demikian, meskipun sering dianggap kompleks, trigonometri memiliki banyak aplikasi praktis yang mempengaruhi kehidupan sehari-hari di berbagai bidang. Pemahaman yang baik tentang konsep dasar trigonometri dapat membuka pintu menuju berbagai penerapan yang berguna dan berharga.